题目内容
9.在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以点C为圆心,5为半径的圆上,连接PA、PB,若PB=4,则PA的长为3或$\sqrt{73}$.分析 连结CP,PB的延长线交⊙C于P′,如图,先计算出CB2+PB2=CP2,则根据勾股定理的逆定理得∠CBP=90°,再根据垂径定理得到PB=P′B=4,接着证明四边形ACBP为矩形,则PA=BC=3,然后在Rt△APP′中利用勾股定理计算出P′A=$\sqrt{73}$,从而得到满足条件的PA的长为3或$\sqrt{73}$.
解答 解: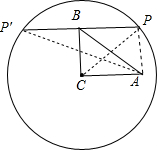 连结CP,PB的延长线交⊙C于P′,如图,
连结CP,PB的延长线交⊙C于P′,如图,
∵CP=5,CB=3,PB=4,
∴CB2+PB2=CP2,
∴△CPB为直角三角形,∠CBP=90°,
∴CB⊥PB,
∴PB=P′B=4,
∵∠C=90°,
∴PB∥AC,
而PB=AC=4,
∴四边形ACBP为矩形,
∴PA=BC=3,
在Rt△APP′中,∵PA=3,PP′=8,
∴P′A=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$,
∴PA的长为3或$\sqrt{73}$.
故答案为3或$\sqrt{73}$.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了垂径定理和勾股定理.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.下列命题是真命题的是( )
| A. | 同旁内角互补 | |
| B. | 一个角的补角大于这个角 | |
| C. | 同位角不相等,两直线不平行 | |
| D. | 如果两个角不相等,那么这两个角不是对顶角 |
14.将四根长度相等的铁丝首尾顺次相接,连成四边形ABCD,转动这个四边形可以使它的形状改变,当∠B=60°时,如图(1),AC=$\sqrt{2}$;当∠B=90°时,如图(2),此时AC的长为( )
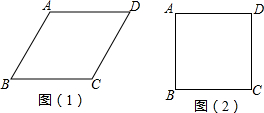
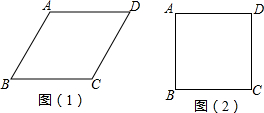
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
1.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与进制的数的对应关系如表:
例如,用十六进制表示5+A=F,3+F=12,E+D=1B,那么A+F=( )
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A. | 1C | B. | 1A | C. | 19 | D. | 21 |
 如图,AD=2,AB=4,∠DAB=45°,BD=BC,BD⊥BC,则AC=6.
如图,AD=2,AB=4,∠DAB=45°,BD=BC,BD⊥BC,则AC=6.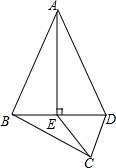 如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )
如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )