题目内容
6. 已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )| A. | $\frac{18}{13}$ | B. | $\frac{20}{13}$ | C. | $\frac{22}{13}$ | D. | $\frac{24}{13}$ |
分析 首先证得四边形BDPM,四边形AFMQ,四边形CEMG均为平行四边形,利用平行线分线段成比例定理可得AD,AE,易得BD,PM,QM,利用平行四边形的性质可得PM,MG,由AA定理易得△QME∽△MPG,利用相似三角形的性质列方程,解得x.
解答 解:∵PQ∥AB,DE∥BC,FG∥AC,
∴四边形BDPM,四边形AFMQ,四边形CEMG均为平行四边形,
∵DE∥BC,
∴$\frac{DE}{BC}=\frac{AD}{AB}=\frac{AE}{AC}$,
∴$\frac{x}{4}=\frac{AD}{2}=\frac{AE}{3}$,
∴AD=$\frac{1}{2}x$,AE=$\frac{3}{4}x$,
∴BD=2-$\frac{1}{2}x$=PM,CE=3-$\frac{3}{4}x$=MG,
∴QM=x-PM=x-2$+\frac{1}{2}x$=$\frac{3}{2}x-2$,
FM=x-MG=x-3$+\frac{3}{4}x$=$\frac{7}{4}x$-3=AQ,
∴QE=$\frac{3}{4}x-\frac{7}{4}x+3$=3-x,
∵FG∥AC,DE∥BC,
∴∠QEM=∠MGP,∠MQE=∠PMG,
∴△QME∽△MPG,
∴$\frac{QM}{PM}=\frac{QE}{MG}$,
∴$\frac{\frac{3}{2}x-2}{2-\frac{1}{2}x}=\frac{3-x}{3-\frac{3}{4}x}$,
解得x=$\frac{24}{13}$.
故选D.
点评 本题主要考查了平行四边形的判定及性质定理和相似三角形的判定及性质定理,能够用x表示出其它边的长是解答此题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
17.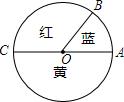 一个转盘的颜色如图所示,其中∠AOB=60°,∠BOC=120°,则转动转盘时,指针落在红色区域的概率是( )
一个转盘的颜色如图所示,其中∠AOB=60°,∠BOC=120°,则转动转盘时,指针落在红色区域的概率是( )
 一个转盘的颜色如图所示,其中∠AOB=60°,∠BOC=120°,则转动转盘时,指针落在红色区域的概率是( )
一个转盘的颜色如图所示,其中∠AOB=60°,∠BOC=120°,则转动转盘时,指针落在红色区域的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
14.下列命题中,正确的是( )
| A. | 正多边形都是中心对称图形 | |
| B. | 经过三角形重心的直线平分三角形的面积 | |
| C. | 在同圆中,相等的弦所对的圆周角相等 | |
| D. | 圆内接平行四边形一定是矩形 |
1.一个寻宝游戏的寻宝通道如图1所示,四边形ABCD为矩形,且AB>AD>$\frac{1}{2}$AB,为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2中的实线所示,则寻宝者的行进路线可能为( )
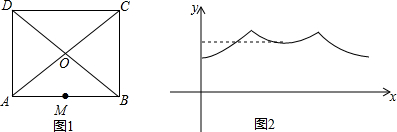

| A. | D→O→C | B. | A→D→C→B | C. | A→D→O→C→B | D. | O→D→C→O |
15.如果2x+5的值与1-4x的值互为相反数,那么x等于( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
16.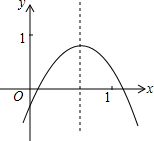 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
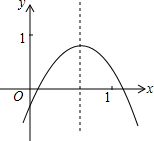 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )| A. | a>0 | B. | abc>0 | C. | a+b+c<0 | D. | b2-4ac<0 |
 如图,直线AB、CD相交与点O,OE是∠AOD的平分线,∠AOC=26°,求:
如图,直线AB、CD相交与点O,OE是∠AOD的平分线,∠AOC=26°,求: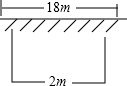 如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,
如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,