题目内容
1.一个寻宝游戏的寻宝通道如图1所示,四边形ABCD为矩形,且AB>AD>$\frac{1}{2}$AB,为记录寻宝者的行进路线,在AB的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2中的实线所示,则寻宝者的行进路线可能为( )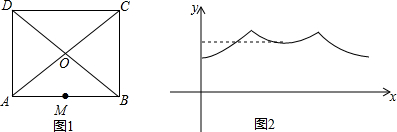
| A. | D→O→C | B. | A→D→C→B | C. | A→D→O→C→B | D. | O→D→C→O |
分析 根据各点到M描点的距离结合图2中的图象可得出结论.
解答 解:A、若D→O→C,则起点距离y最远,不符合图2中起点的位置,故本选项错误;
B、若A→D→C→B,则A、B为最低点,D、C为最高点,符合题意,故本选项正确;
C、若A→D→O→C→B,则到达CD两点时y最大,到达O点时,y最小,由图可知在起点和终点时y最小,故本选项错误;
D、若O→D→C→O,则两最高点间弧线部分的最低点y的值恰好等于起点y值的两倍,故本选项错误.
故选B.
点评 本题考查的是动点问题的函数图象,根据正方形各边的关系结合x与y的关系求解是解答此题的关键.

练习册系列答案
相关题目
11.下列式子计算一定正确的是( )
| A. | 3x2-5x2=-2x | B. | 6x2+2x2=3x2 | C. | x2+x2=2x2 | D. | -2(x-2)=-2x-4 |
6. 已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
 已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )| A. | $\frac{18}{13}$ | B. | $\frac{20}{13}$ | C. | $\frac{22}{13}$ | D. | $\frac{24}{13}$ |
11.长春市某校准备组织教师、学生、家长到大连进行参观学习活动,旅行社代办购买动车票,动车票价格如下表所示:
根据报名总人数,若所有人员都买一等座的动车票,则共需13650元;若都买二等座动车票(学生全部按表中的“学生票二等座”购买),则共需8820元.已知家长的人数是教师的人数的2倍.
(1)设参加活动的老师有m人,则教师和家长按照成人票价的一等座购买动车票的总费用是195m元(用含有m的代数式表示);
(2)设参加活动的学生有n人,求参加活动的老师、家长及学生分别有多少人?
(3)如果二等座动车票共买到x张,且学生全部按表中的“学生票二等座”购买,其余的买一等座动车票,且买票的总费用不低于9000元,直接写出x的最大值是193.
| 运行区间 | 成人票价 | 学生票 | ||
| 出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
| 长春 | 大连 | 65(元) | 54(元) | 40(元) |
(1)设参加活动的老师有m人,则教师和家长按照成人票价的一等座购买动车票的总费用是195m元(用含有m的代数式表示);
(2)设参加活动的学生有n人,求参加活动的老师、家长及学生分别有多少人?
(3)如果二等座动车票共买到x张,且学生全部按表中的“学生票二等座”购买,其余的买一等座动车票,且买票的总费用不低于9000元,直接写出x的最大值是193.
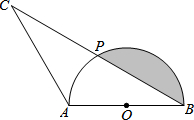 如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC.
如图,已知AB是半圆O的直径,点P是半圆上一点,连结BP,并延长BP到点C,使PC=PB,连结AC. 如图是一张长方形硬纸片,正好分成15个完全相同的小正方形,现要把它们剪切成3份,使每份有5个小正方形相连,折起来都可以围成一个没有盖的正方体纸盒.请在图中用实线画出一种剪切线.
如图是一张长方形硬纸片,正好分成15个完全相同的小正方形,现要把它们剪切成3份,使每份有5个小正方形相连,折起来都可以围成一个没有盖的正方体纸盒.请在图中用实线画出一种剪切线.