题目内容
18.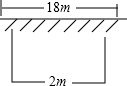 如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,
如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,(1)若设长方形的长(与墙平行的矩形边长)为x米,那么与墙垂直的竹篱笆的长是$\frac{1}{2}$(35-x)米?
(2)按(1)的设法,求鸡场的长和宽各为多少米.
分析 (1)设长方形的长(与墙平行的矩形边长)为x米,用总长减去一个长后除以2即可求得与墙垂直的墙长;
(2)根据面积为150平方米结合矩形的面积列出方程求解即可.
解答 解:(1)∵墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,
∴篱笆总长为33+2=35米,
设长方形的长(与墙平行的矩形边长)为x米,那么与墙垂直的竹篱笆的长是$\frac{1}{2}$(35-x)米,
故答案为:$\frac{1}{2}$(35-x);
(2)根据题意得:$\frac{1}{2}$(35-x)x=150,
解得:x=15或x=20,
∵x=20>18,
∴x=15,
当x=15时,$\frac{1}{2}$(35-15)=10米;
答:篱笆的长为15米,宽为10米.
点评 本题考查了一元二次方程的应用,解题的关键是根据题意表示出矩形的长和宽,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
 已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )| A. | $\frac{18}{13}$ | B. | $\frac{20}{13}$ | C. | $\frac{22}{13}$ | D. | $\frac{24}{13}$ |
3.下列方程中,是一元一次方程的是( )
| A. | x2-4x=3 | B. | 2x+5=3(x-1) | C. | x+2y=1 | D. | xy-3=5 |
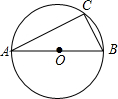 如图,AB是⊙O的直径,点C是⊙O上一点,若BC=1,AC=2,则OB的长度是$\frac{\sqrt{5}}{2}$.
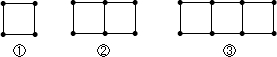
如图,AB是⊙O的直径,点C是⊙O上一点,若BC=1,AC=2,则OB的长度是$\frac{\sqrt{5}}{2}$. 如图是一张长方形硬纸片,正好分成15个完全相同的小正方形,现要把它们剪切成3份,使每份有5个小正方形相连,折起来都可以围成一个没有盖的正方体纸盒.请在图中用实线画出一种剪切线.
如图是一张长方形硬纸片,正好分成15个完全相同的小正方形,现要把它们剪切成3份,使每份有5个小正方形相连,折起来都可以围成一个没有盖的正方体纸盒.请在图中用实线画出一种剪切线.