题目内容
1.已知x2-3x+1=0,求下列各式的值:(1)x2+$\frac{1}{{x}^{2}}$;
(2)$\frac{{x}^{6}+3{x}^{3}+1}{2{x}^{3}}$.
分析 (1)利用方程先求出x+$\frac{1}{x}$=3,把x2+$\frac{1}{{x}^{2}}$化为(x+$\frac{1}{x}$)2-2求解即可,
(2)把$\frac{{x}^{6}+3{x}^{3}+1}{2{x}^{3}}$化为$\frac{1}{2}$×[(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)+3求解即可
解答 解:∵x2-3x+1=0,
∴x-3+$\frac{1}{x}$=0,即x+$\frac{1}{x}$=3,
(1)x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=7;
(2)$\frac{{x}^{6}+3{x}^{3}+1}{2{x}^{3}}$=$\frac{1}{2}$×(x3+3+$\frac{1}{{x}^{3}}$)=$\frac{1}{2}$×[(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)+3]=$\frac{1}{2}$×[3×6+3]=$\frac{21}{2}$.
点评 本题主要考查了分式的混合运算,解题的关键是正确求出x+$\frac{1}{x}$=3.

练习册系列答案
相关题目
11. 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“我”字所在的面相对的面上标的字是( )| A. | 中 | B. | 国 | C. | 的 | D. | 梦 |
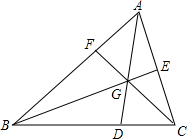 如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.
如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G,BC=3DC,S△GEC=3,S△GBD=8,则△ABC的面积是30.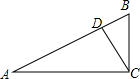 如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.
如图,在△ABC中,∠ACB=90°,D为AB边上一点,∠BCD=35°,∠BDC=80°.求∠A的度数.