题目内容
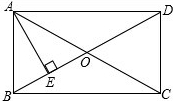 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.(1)求∠BAE的度数;
(2)AE等于多少?
考点:矩形的性质,勾股定理
专题:
分析:(1)由在矩形ABCD中,AE⊥BD于E,BE:ED=1:3,易证得△OAB是等边三角形,继而求得∠BAE的度数;
(2)由△OAB是等边三角形,易求得∠ADE=30°,又由AD=6,即可求得AE的长.
(2)由△OAB是等边三角形,易求得∠ADE=30°,又由AD=6,即可求得AE的长.
解答:解:(1)∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠BAE=30°;
(2)∵△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°-∠ABD=30°,
∵AE⊥BD,AD=6,
∴AE=
AD=3.
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠BAE=30°;
(2)∵△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°-∠ABD=30°,
∵AE⊥BD,AD=6,
∴AE=
| 1 |
| 2 |
点评:此题考查了矩形的性质、等边三角形的判定与性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 如图,AD=BD=CD,∠CBD=20°,则∠BAC=( )
如图,AD=BD=CD,∠CBD=20°,则∠BAC=( )| A、40° | B、60° |
| C、70° | D、80° |

 在直径为200cm的圆柱形油箱内装入一些油以后,截面如图(油面在圆心下):若油面的宽AB=160cm,则油的最大深度为
在直径为200cm的圆柱形油箱内装入一些油以后,截面如图(油面在圆心下):若油面的宽AB=160cm,则油的最大深度为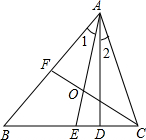 如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.
如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.