题目内容
三角形三边分别为5,12,13,那么最长边上的高为 .
考点:勾股定理的逆定理
专题:
分析:根据勾股定理的逆定理求出三角形是直角三角形,根据三角形面积公式求出即可.
解答:解:∵52+122=132,
∴三角形是直角三角形,
设最长边上的高为h,
由三角形面积公式得:
×5×12=
×13×h,
解得:h=
,
故答案为:
.
∴三角形是直角三角形,
设最长边上的高为h,
由三角形面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:h=
| 60 |
| 13 |
故答案为:
| 60 |
| 13 |
点评:本题考查了三角形的面积公式和勾股定理的逆定理的应用,解此题的关键是能推出三角形是直角三角形,难度适中.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
把方程3x(x-1)=5(x+2)化为一般形式正确的是( )
| A、3x2-3x-10=0 |
| B、3x2-8x-10=0 |
| C、3x2-8x+10=0 |
| D、x2-3x-10=0 |
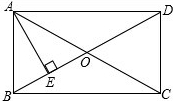 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.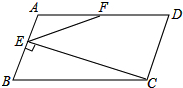 如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值.
如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值.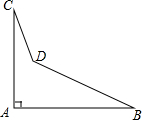 一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.
一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.