题目内容
在直径为200cm的圆柱形油箱内装入一些油以后，截面如图（油面在圆心下）：若油面的宽AB=160cm，则油的最大深度为考点：垂径定理的应用,勾股定理
专题：
分析：连接OA，过点O作OE⊥AB，交AB于点M，由垂径定理求出AM的长，再根据勾股定理求出OM的长，进而可得出ME的长．
解答：
40cm解：连接OA，过点O作OE⊥AB，交AB于点M，
∵直径为200cm，AB=160cm，
∴OA=OE=100cm，AM=80cm，
∴OM=
=
=60cm，
∴ME=OE-OM=100-60=40cm．
故答案为40cm．
40cm解：连接OA，过点O作OE⊥AB，交AB于点M，∵直径为200cm，AB=160cm，
∴OA=OE=100cm，AM=80cm，
∴OM=
| OA2-AM2 |
| 1002-802 |
∴ME=OE-OM=100-60=40cm．
故答案为40cm．
点评：本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
已知点A的坐标为（1，4），则点A关于y轴对称的点的横坐标为（ ）
| A、1 | B、-1 | C、4 | D、-4 |
小明设计了某个产品的包装盒，由于粗心，少设计了其中一部分，请你把它补上，使其成为一个两面均有盖的正方体盒子，共有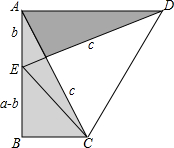
如图，两个全等的直角△ABC和△DAE，两直角边的长分别为a，b，斜边长为c，使用两种不同的方法表示梯形ABCD的面积，并以此来验证勾股定理．
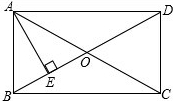如图，在矩形ABCD中，对角线AC与BD相交于点O，AE⊥BD于E，若BE：ED=1：3，AD=6．
如图，在宽为30m，长为40m的矩形地面上修建两条同样宽的道路，余下部分作为耕地．根据图中数据，计算耕地的面积为（ ）| A、1200m2 |
| B、1131m2 |
| C、1181 m2 |
| D、1209m2 |
某人A地出发，先去小河l边饮马，然后B地办事，欲使所走路程最短，求饮马的位置应选在何处，说明理由．在以下四个图案中，是轴对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |