题目内容
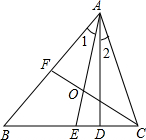 如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.
如图,△ABC中,∠C>∠B,AE为角平分线,AD⊥BC于D.(1)求证:∠EAD=
| 1 |
| 2 |
(2)当垂足D点在直线BC上运动时(不与点E重全),垂线交直线AE于A′,其他条件不变画出相应的图形,并指出与在(1)相应的结论是什么?是否仍成立?
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠BAE,然后根据直角三角形两锐角互余求出∠BAD,最后根据∠EAD=∠BAD-∠BAE代入即可得解;
(2)按要求画出图形,与在(1)相应的结论是∠EA′D=
(∠C-∠B),类比(1)的求法得出答案即可.
(2)按要求画出图形,与在(1)相应的结论是∠EA′D=
| 1 |
| 2 |
解答:(1)证明:在△ABC中,∠BAC=180°-∠B-∠ACB,
∵AE平分∠BAC交BC于E,
∴∠1=∠BAC=
(180°-∠B-∠C)=90°-
(∠B+∠C),
∵∠B=40°,AD⊥BC,
∴∠BAD=90°-∠B,
∴∠EAD=∠BAD-∠BAE=90°-∠B-90°+
(∠B+∠C)=
(∠C-∠B).
(2)如图所示,
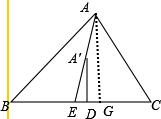
过点A作AG⊥BC于点G,则A′D∥AG,∠DA′E=∠EAG,
∵∠AGC=90°,
∴∠CAG=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C,
∵∠BAE=∠CAE,
∴∠CAE=
∠BAC=
(180°-∠B-∠C)=90°-
(∠B+∠C).
∵∠EAG=∠CAE-∠CAG=90°-
(∠B+∠C)-(90°-∠C)
=
(∠C-∠B),
∴∠EA′D=
(∠C-∠B).
∵AE平分∠BAC交BC于E,
∴∠1=∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠B=40°,AD⊥BC,
∴∠BAD=90°-∠B,
∴∠EAD=∠BAD-∠BAE=90°-∠B-90°+
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图所示,

过点A作AG⊥BC于点G,则A′D∥AG,∠DA′E=∠EAG,
∵∠AGC=90°,
∴∠CAG=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C,
∵∠BAE=∠CAE,
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠EAG=∠CAE-∠CAG=90°-
| 1 |
| 2 |
=
| 1 |
| 2 |
∴∠EA′D=
| 1 |
| 2 |
点评:本题主要考查了三角形的内角和定理和三角形的高、角平分线的性质,学生应熟练掌握三角形的高、中线和角平分线这些基本知识,能灵活运用解决问题.

练习册系列答案
相关题目
 如图,在以BD为直径的⊙O上,
如图,在以BD为直径的⊙O上, |
| AB |
 |
| BC |
| A、70° | B、30° |
| C、35° | D、40° |
在以下四个图案中,是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6. 某人A地出发,先去小河l边饮马,然后B地办事,欲使所走路程最短,求饮马的位置应选在何处,说明理由.
某人A地出发,先去小河l边饮马,然后B地办事,欲使所走路程最短,求饮马的位置应选在何处,说明理由. 如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值.
如图,?ABCD中,BC=2CD,CE⊥AB于点E,F为AD的中点,若∠EFD=k∠AEF,求k的值. 一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.
一个零件的形状如图,按规定∠A应等于90°,∠B与∠C应分别是32°和21°,检验工人量得∠BDC=148°,就判断这个零件不合格,试用三角形的有关知识说明理由.