题目内容
4.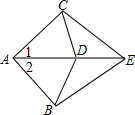 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )| A. | ∠1=∠2 | B. | AD=DE | C. | BD=CD | D. | ∠BDE=∠CDE |
分析 根据已知条件证得△ABE≌△ACE,得到∠1=∠2,故A正确,进一步证得△ACD≌△ABD,得到BD=CD,故B正确,于是得到∠BDE=∠CDE,故D正确.
解答 解:在△ABE与△ACE中,$\left\{\begin{array}{l}{AB=AC}\\{BE=CE}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ACE,
∴∠1=∠2,故A正确,
在△ACD与△ABD中,$\left\{\begin{array}{l}{AC=AB}\\{∠1=∠2}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△ABD,
∴BD=CD,故C正确,
∵△ACD≌△ABD,
∴∠ADC=∠ADB,
∴∠BDE=∠CDE,故D正确,
故选B.
点评 本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
15.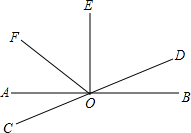 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )
 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )| A. | ∠AOF=45° | B. | ∠AOD与∠BOD互为补角 | ||
| C. | ∠BOD=∠AOC | D. | ∠BOD的余角等于85° |
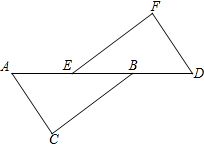 已知如图:AE=DB,∠C=∠F,BC∥EF,求证:△ABC≌△DEF.
已知如图:AE=DB,∠C=∠F,BC∥EF,求证:△ABC≌△DEF.
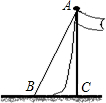 如图,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
如图,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.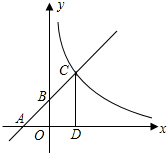 如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3,
如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3, 如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值.
如图是一个正方体的展开图,标注了字母A的面是正方体的正面,如果正方体的左面与右面所标注式子的值相等,求x的值.