题目内容
14.李华同学上学期期末考试数学成绩为76分,他平时考试数学成绩为90分,期中考试数学成绩为80分.(1)请问他上学期的数学平均成绩是多少?
(2)如果期末总评成绩按平时成绩占20%,期中成绩占30%,期末成绩占50%计算,那么李华同学上学期期末总评数学成绩是多少?
分析 (1)直接利用算术平均数的计算公式计算即可;
(2)利用加权平均数的计算公式进行计算即可.
解答 解:(1)数学平均成绩为:$\frac{1}{3}$(76+90+80)=82分;
(2)李华同学上学期期末总评数学成绩是90×20%+80×30%+76×50%=18+24+38=80分.
点评 本题考查的是加权平均数的求法.熟记公式是解决本题的关键.解题时要认真审题,不要把数据代错.

练习册系列答案
相关题目
4.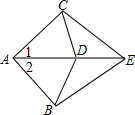 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )| A. | ∠1=∠2 | B. | AD=DE | C. | BD=CD | D. | ∠BDE=∠CDE |
5.2010年6月5日是第38个世界环境日,世界环境日的主题为“多个物种、一颗星球、一个未来”.为了响应节能减排的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共16辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:
(1)若经营者的购买资金不少于576万元且不多于600万元,则有哪几种进车方案?
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.
| 成本价(万元/辆) | 售价(万元/辆) | |
| A型 | 30 | 32 |
| B型 | 42 | 45 |
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.
2.不等式y+2≤3的正整数解为( )
| A. | 1,2 | B. | 2,3 | C. | 2 | D. | 1 |
19.若分式$\frac{x+1}{x-5}$有意义,则x的取值范围是( )
| A. | x=1 | B. | x=5 | C. | x≠1 | D. | x≠5 |
3.下列等式是由3x=4x-1根据等式性质变形得到的,其中正确的个数有( )
①4x-3x=1;②3x-4x=1;③$\frac{3}{2}x=2x-\frac{1}{2}$;④-1=3x+4x.
①4x-3x=1;②3x-4x=1;③$\frac{3}{2}x=2x-\frac{1}{2}$;④-1=3x+4x.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.计算(2+1)(22+1)(24+1)(28+1)得( )
| A. | 216-1 | B. | 29+1 | C. | 29-1 | D. | 216+1 |