题目内容
3.计算:$\frac{1}{a-x}$-$\frac{1}{a+x}$-$\frac{2x}{{a}^{2}+{x}^{2}}$-$\frac{4{x}^{3}}{{a}^{4}+{x}^{4}}$+$\frac{8{x}^{7}}{{x}^{8}-{a}^{8}}$.分析 原式通分并利用同分母分式的加减法则计算即可得到结果.
解答 解:原式=$\frac{a+x-a+x}{{a}^{2}-{x}^{2}}$-$\frac{2x}{{a}^{2}+{x}^{2}}$-$\frac{4{x}^{3}}{{a}^{4}+{x}^{4}}$+$\frac{8{x}^{7}}{{x}^{8}-{a}^{8}}$=$\frac{4{x}^{3}}{{a}^{4}-{x}^{4}}$-$\frac{4{x}^{3}}{{a}^{4}+{x}^{4}}$+$\frac{8{x}^{7}}{{x}^{8}-{a}^{8}}$=$\frac{8{x}^{7}}{{a}^{8}-{x}^{8}}$+$\frac{8{x}^{7}}{{x}^{8}-{a}^{8}}$=$\frac{8{x}^{7}-8{x}^{7}}{{a}^{8}-{x}^{8}}$=0.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.当分式$\frac{x+2}{x-1}$的值为0时,x的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
15.若“!”是一种运算符号,并且1!=1,2!=2×1,3!=3×2×1,…,则$\frac{99!}{97!}$=( )
| A. | $\frac{99}{97}$ | B. | 98! | C. | 9702 | D. | 2! |
4.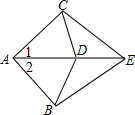 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )| A. | ∠1=∠2 | B. | AD=DE | C. | BD=CD | D. | ∠BDE=∠CDE |