题目内容
9.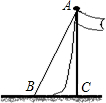 如图,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
如图,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.
分析 设旗杆的高度是x米,绳子长为(x+1)米,旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求出x的值,从而求出旗杆的高度.
解答 解:设旗杆的高度为xm,根据题意可得:
(x+1)2=x2+52,
解得:x=12,
答:旗杆的高度为12m.
点评 本题考查勾股定理的应用,关键看到旗杆,拉直的绳子和BC构成直角三角形,根据勾股定理可求解.

练习册系列答案
相关题目
4.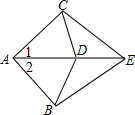 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )| A. | ∠1=∠2 | B. | AD=DE | C. | BD=CD | D. | ∠BDE=∠CDE |
1.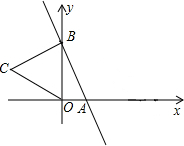 如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
 如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
19.若分式$\frac{x+1}{x-5}$有意义,则x的取值范围是( )
| A. | x=1 | B. | x=5 | C. | x≠1 | D. | x≠5 |
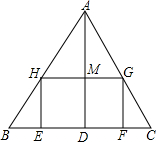 如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.
如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.
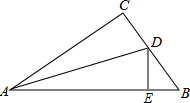 如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若DB=2cm,则DC=$\sqrt{2}$cm.
如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若DB=2cm,则DC=$\sqrt{2}$cm.