题目内容
12.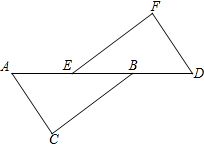 已知如图:AE=DB,∠C=∠F,BC∥EF,求证:△ABC≌△DEF.
已知如图:AE=DB,∠C=∠F,BC∥EF,求证:△ABC≌△DEF.证明∵BC∥EF(已知)
∴∠ABC=∠DEF(两直线平行,内错角相等)
∵AE=DB (已知)
∴AE+BE=DB+BE
即:AB=DE(等式性质)…(请你把题目续证完)
分析 由平行线的性质和等式的性质得出∠ABC=∠DEF,AB=DE,由AAS证明△ABC≌△DEF即可.
解答 解:∵BC∥EF(已知)
∴∠ABC=∠DEF(两直线平行,内错角相等)
∵AE=DB (已知)
∴AE+BE=DB+BE,
即:AB=DE(等式性质),
在△ABC和△DEF中,$\left\{\begin{array}{l}{∠C=∠F}&{\;}\\{∠ABC=∠DEF}&{\;}\\{AB=DE}&{\;}\end{array}\right.$,
∴△ABC和△DEF(AAS);
故答案为:∠ABC,∠DEF;BE,BE;DE.
点评 本题考查了平行线的性质、等式的性质、全等三角形的判定方法;熟练掌握平行线的性质和三角形全等的判定方法,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
7.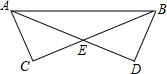 已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
 已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )| A. | ∠ABC=∠BAD | B. | AC=BD | C. | ∠CAB=∠DBA | D. | ∠C=∠D=90° |
4.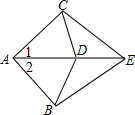 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )| A. | ∠1=∠2 | B. | AD=DE | C. | BD=CD | D. | ∠BDE=∠CDE |
1.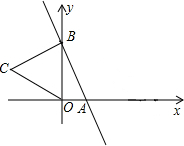 如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
 如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
2.不等式y+2≤3的正整数解为( )
| A. | 1,2 | B. | 2,3 | C. | 2 | D. | 1 |
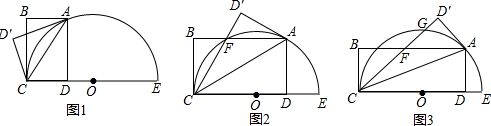
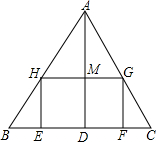 如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.
如图,△ABC,是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm,从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC,AB上,AD与HG的交点为M.