题目内容
16.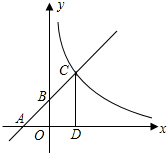 如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3,
如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3,(1)求点A,B,D的坐标;
(2)求一次函数和反比例函数的解析式.
分析 (1)根据OA=OB=OD=3和各坐标轴上的点的特点易得到所求点的坐标;
(2)将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式,由C点在一次函数的图象上可确定C点坐标,将C点坐标代入y=$\frac{m}{x}$(m≠0)可确定反比例函数的解析式.
解答 解:(1)∵OA=OB=OD=3,
∴点A、B、D的坐标分别为A(-3,0),B(0,3),D(3,0);
(2)∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴一次函数的解析式为y=x+3.
∵点C在一次函数y=x+3的图象上,且CD⊥x轴,
∴点C的坐标为(3,6),
又∵点C在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,
∴m=18;
∴反比例函数的解析式为y=$\frac{18}{x}$.
点评 本题主要考查用待定系数法求函数解析式,过某个点,这个点的坐标应适合这个函数解析式.

练习册系列答案
相关题目
15.若“!”是一种运算符号,并且1!=1,2!=2×1,3!=3×2×1,…,则$\frac{99!}{97!}$=( )
| A. | $\frac{99}{97}$ | B. | 98! | C. | 9702 | D. | 2! |
7.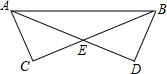 已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
 已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )| A. | ∠ABC=∠BAD | B. | AC=BD | C. | ∠CAB=∠DBA | D. | ∠C=∠D=90° |
4.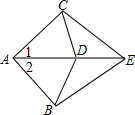 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
 如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )
如图,已知AB=AC,BE=CE,D是AE上的一点,则下列结论不一定成立的是( )| A. | ∠1=∠2 | B. | AD=DE | C. | BD=CD | D. | ∠BDE=∠CDE |
1.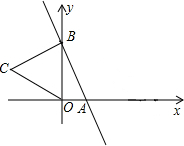 如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
 如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
如图,直线y=-2x+6与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将点C向右平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为($\frac{3}{2}$,3).
5.2010年6月5日是第38个世界环境日,世界环境日的主题为“多个物种、一颗星球、一个未来”.为了响应节能减排的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共16辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:
(1)若经营者的购买资金不少于576万元且不多于600万元,则有哪几种进车方案?
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.
| 成本价(万元/辆) | 售价(万元/辆) | |
| A型 | 30 | 32 |
| B型 | 42 | 45 |
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.
 如图所示,△ABC为等边三角形,AD∥BC,CD⊥AD,若△ABC的周长为36cm,则AD的长为6cm.
如图所示,△ABC为等边三角形,AD∥BC,CD⊥AD,若△ABC的周长为36cm,则AD的长为6cm. 如图,在⊙O中,∠AOC=∠BOC,过点C分别作半径OA、OB的垂线,垂足分别为M、N,交⊙O于E、F两点,求证:ME=NF.
如图,在⊙O中,∠AOC=∠BOC,过点C分别作半径OA、OB的垂线,垂足分别为M、N,交⊙O于E、F两点,求证:ME=NF.