题目内容
2.抛物线y=-3x2+2x-l的图象与坐标轴交点的个数是( )| A. | 没有交点 | B. | 只有一个交点 | C. | 两个交点 | D. | 三个交点 |
分析 先根据根的判别式求出与x轴的交点,再求出与y轴的交点,即可得出选项.
解答 解:y=-3x2+2x-l,
∵b2-4ac=22-4×(-3)×(-1)=16>0,
∴抛物线y=-3x2+2x-l的图象与x轴交点的个数是2,
与y轴的交点是(0,-1),
2+1=3,
故选D.
点评 本题考查了抛物线与x轴的交点的应用,能理解如何求抛物线和坐标轴的交点坐标是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.一影院观众席中的9排23号记作(9,23),那么15排42号的位置应记作( )
| A. | (42,15) | B. | (1,4) | C. | (15,42) | D. | (15,4) |
10.对于一次函数y=-2x+4,下列结论错误的是( )
| A. | 函数值随自变量的增大而减小 | |
| B. | 当x<0时,y<4 | |
| C. | 函数的图象向下平移4个单位长度得y=-2x的图象 | |
| D. | 函数的图象与y轴的交点坐标是(0,4) |
17. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )| A. | 8+6$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 19.2 | D. | 20 |
12.一次函数y=4x-2的图象可以由正比例函数y=4x的图象( )得到.
| A. | 向上平移2个单位 | B. | 向下平移4个单位 | C. | 向下平移2个单位 | D. | 向上平移4个单位 |
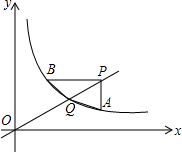 如图,直线y=mx与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点A,点B都在反比例函数y=$\frac{k}{x}$的图象上,点P在OQ延长线上,且PA∥y轴,PB∥x轴,且连结AQ,BQ,已知B(3,4).
如图,直线y=mx与反比例函数y=$\frac{k}{x}$(x>0)的图象交于Q点,点A,点B都在反比例函数y=$\frac{k}{x}$的图象上,点P在OQ延长线上,且PA∥y轴,PB∥x轴,且连结AQ,BQ,已知B(3,4).