题目内容

13．求证：平行四边形一组对边中点的连线必与对角线互相平分．

分析 根据题意画出图形，写出已知，求证；证明四边形AFCE是平行四边形，得出EF与AC互相平分，同理：EF与BD互相平分．

解答 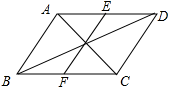如图所示：已知平行四边形ABCD中，E、F分别是AD、BC的中点，
求证：EF与AC互相平分，EF与BD互相平分；
证明：连接AF、CE，
如图：
∵四边形ABCD是平行四边形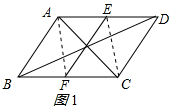
∴AD∥BC，AD=BC，
∵E、F分别是AD、BC的中点，
∴AE=CF=DE=BF，
又∵AD∥BC，
∴四边形AFCE是平行四边形，∴EF与AC互相平分，
同理：EF与BD互相平分．

点评 本题考查了平行四边形的判定与性质；熟练掌握平行四边形的判定与性质，证明四边形AFCE是平行四边形是解决问题的关键．

练习册系列答案
相关题目
3．如图，点A，B，C都在⊙O上，若∠OAC=17°，∠ACB=46°，AC与OB交于点D，则∠ODA的度数为71度．
4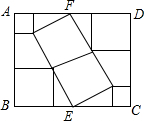．如图，在矩形ABCD内放入六个小正方形后形成一个中心对称图形，其中顶点E、F分别在边BC、AD上，则长AD与宽AB的比值为（　　）
A．6：5B．13：10C．8：7D．4：3
1．已知，在平面直角坐标系中，A（m-2，a），B（m+2，b），且有理数a，b满足a+2+$\sqrt{2}$b=4$\sqrt{2}$+b．
（1）试求出a，b的值，并直接写出以AB为对角线的平行四边形AOBC的第四顶点C的纵坐标；
（2）若△AOB的面积为9，求m的值；
（3）若直线AB与x轴交于点D，当线段AB平移时，△ABC的面积：△AOD的面积是否是定值？若是定值，请求出该值，并说明理由；若不是，请指出它的范围．
8．（1）如图1，已知△ABC，∠C=90°，AC＜BC，D为BC上一点，且到A，B两点的距离相等，用尺规作出点D的位置；
（2）如图2，已知△ABC，∠A=90°，用尺规作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切；
（3）如图3，用尺规过点A作BC边的垂线MN，交BC于点D．
18．如图是一服装包装袋挂于墙上的示意图，绳子BAC挂在墙上支点A处，为使包装袋平衡，绳子均匀的挂在A点处（即AB=AC），绳子的总长为30cm，此时绳子与水平线夹角为72°．
（1）求袋子两支点BC的距离；
（2）为了让包装袋离地面更远，先在绳子上打一个结，然后均匀的挂在A点处，使得绳子与水平线的夹角为30°，求绳子减少的长度（结果精确到0.1cm，参考数据：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08，$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）．
5．如图1所示，在?ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿射线AC的方向匀速平移得到△PNM，速度为1cm/s，同时，点Q从点C出发，沿射线CB方向匀速运动，速度为1cm/s，当△PNM停止平移时，点Q也停止运动，如图2所示，设运动时间为t（s）（0＜t＜4）．
（1）当t为何值时，PQ∥MN？
（2）设△QMC的面积为y（cm2），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使得PQ=QM，若存在，求出t的值；若不存在，请说明理由．
13．一元二次方程x2-2x-6=0，其中较大的一个根为x1，下列最接近x1的范围是（　　）
A．3＜x1＜4B．3＜x1＜3.5C．3.5＜x1＜3.7D．3.7＜x1＜4
14．一个三角形的两边长为8和10，则它的最长边的取值范围是10≤a＜18．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网