题目内容
4．
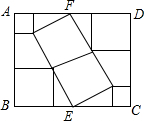如图，在矩形ABCD内放入六个小正方形后形成一个中心对称图形，其中顶点E、F分别在边BC、AD上，则长AD与宽AB的比值为（ ）| A． | 6：5 | B． | 13：10 | C． | 8：7 | D． | 4：3 |
分析 连结EF，作IJ⊥LJ于J，根据中心对称图形的定义和相似三角形的性质可得两直角边的比是2：1，进一步得到长AD与宽AB的比．
解答 
解：连结EF，作IJ⊥LJ于J，
∵在矩形ABCD内放入六个小正方形后形成一个中心对称图形，
∴△HGF∽△FHE，△HGF≌△FML≌△LJI，
∴HG：GF=FH：HE=1：2，
∴长AD与宽AB的比为（1+2+1+2）：（2+2+1）=6：5．
故选：A．
点评 此题考查了中心对称图形，相似三角形的性质，关键是理解直角三角形两直角边的比是2：1．
练习册系列答案
相关题目
如图，△ABC各顶点的坐标分别为A（-1，-1）、B（5，3）、C（1，4）．
如图，已知直线y1=x+m与x轴、y轴分别交于点A、B，与双曲线y2=$\frac{k}{x}$（x＜0）分别交于点C（-1，2）、D（a，1）．
如图，直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为2，等腰△ABC的顶点分别在直线l1、l2，l3上，AB=AC，∠BAC=120°，则等腰三角形的腰长为2或$\frac{2\sqrt{39}}{3}$或$\frac{2\sqrt{57}}{3}$．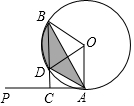
如图，已知PA为⊙O的切线，A为切点，B为⊙O上一点，∠AOB=120°，过点B作BC⊥PA于点C，BC交⊙O于点D，连接AB、AD．