题目内容
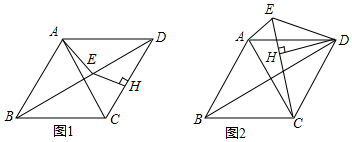
5.如图1所示,在?ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.

分析 (1)如图1,先根据题意得:CQ=AP=t,利用勾股定理求AC的长,根据PQ∥AB,列比例式可求得t的值;
(2)如图2,作辅助线,构建相似三角形,利用面积法得:S△ABC=$\frac{1}{2}$AB×AC=$\frac{1}{2}$AE×BC,可得:AE=$\frac{12}{5}$,由勾股定理易得:CE=$\frac{16}{5}$.证明△CPD∽△CAE,列比例式$\frac{CP}{CA}=\frac{CD}{CE}=\frac{PD}{AE}$,求PD和CD的长,根据面积公式求△QCM的面积y;
(3)如图3,作辅助线,构建相似三角形,证明△CQH∽△CAB,列比例式得:$\frac{CQ}{CA}=\frac{CH}{CB}$,表示CH=$\frac{5}{4}$t,则PH=AC-AP-CH=4-$\frac{9}{4}$t,易证△PHD∽△CBA,列式可求得t的值.
解答  (1)如图1,由题意得:CQ=AP=t,
(1)如图1,由题意得:CQ=AP=t,
在Rt△ABC中,由勾股定理得AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴CP=4-t,
由平移的性质可得MN∥AB,
∵PQ∥MN,
∴PQ∥AB,
∴$\frac{CP}{AC}=\frac{CQ}{BC}$,即$\frac{4-t}{4}=\frac{t}{5}$,
解得t=$\frac{20}{9}$,
则当t为何值时,PQ∥MN;
(2)如图2,过点P作PF⊥BC于点F,过点A作AE⊥BC于点E,
由S△ABC=$\frac{1}{2}$AB×AC=$\frac{1}{2}$AE×BC,
$\frac{1}{2}$×3×4=$\frac{1}{2}$×5AE,
可得:AE=$\frac{12}{5}$,
则由勾股定理易得:CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$.
∵PD⊥BC,AE⊥BC,
∴AE∥PD,
∴△CPD∽△CAE,
∴$\frac{CP}{CA}=\frac{CD}{CE}=\frac{PD}{AE}$,即$\frac{4-t}{4}=\frac{CD}{\frac{16}{5}}=\frac{PD}{\frac{12}{5}}$
∴PD=$\frac{12-3t}{5}$,CD=$\frac{16-4t}{5}$,
∵PM∥BC,
∴点M到BC的距离h=PD=$\frac{12-3t}{5}$,
∴△QCM的面积y=$\frac{1}{2}$CQ×h=$\frac{1}{2}$×$t×\frac{12-3t}{5}$=-$\frac{3}{10}{t}^{2}$+$\frac{6}{5}t$(0<t<4);
(3)如图3,过点Q作QD⊥PM于点D,QD交AC于点H.
∵PQ=MQ,
∴PD=DM=$\frac{5}{2}$,且DQ⊥BC.
在Rt△ABC中,AC=4,AP=t,QC=t.
∵∠A=∠HQC,∠ACB=∠QCH,
∴△CQH∽△CAB,
∴$\frac{CQ}{CA}=\frac{CH}{CB}$,即$\frac{t}{4}=\frac{CH}{5}$,
∴CH=$\frac{5}{4}$t,
∴PH=AC-AP-CH=4-t-$\frac{5}{4}$t=4-$\frac{9}{4}$t,
易证△PHD∽△CBA,
∴$\frac{PH}{BC}=\frac{PD}{AC}$,
即$\frac{4-\frac{9}{4}t}{5}=\frac{\frac{5}{2}}{4}$,
解得t=$\frac{7}{18}$.
∴当t=$\frac{7}{18}$时,PQ=QM.
点评 本题是四边形的综合题,考查了动点运动问题、三角形相似的性质和判定、勾股定理,熟练掌握平行相似的判定是关键,注意三角形PMN运动时可以看作是点P从A运动到C,利用数形结合的思想.

 如图,半径为5的⊙A中,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长为( )
如图,半径为5的⊙A中,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长为( )| A. | $\sqrt{41}$ | B. | $\sqrt{61}$ | C. | 11 | D. | 8 |
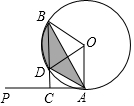 如图,已知PA为⊙O的切线,A为切点,B为⊙O上一点,∠AOB=120°,过点B作BC⊥PA于点C,BC交⊙O于点D,连接AB、AD.
如图,已知PA为⊙O的切线,A为切点,B为⊙O上一点,∠AOB=120°,过点B作BC⊥PA于点C,BC交⊙O于点D,连接AB、AD.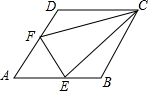 如图,菱形ABCD中,∠A=60°,点E、F分别是边AB、AD上的点,且满足∠BCE=∠DCF,连接EF,当AF=$\sqrt{5}$时,求EF的长.
如图,菱形ABCD中,∠A=60°,点E、F分别是边AB、AD上的点,且满足∠BCE=∠DCF,连接EF,当AF=$\sqrt{5}$时,求EF的长.