题目内容
20.已知两个函数,如果对于任意的自变量x,这两个函数对应的函数值记为y1,y2,都有点(x,y1)、(x,y2)关于点(x,x)对称,则称这两个函数为关于y=x的对称函数,例如,y1=$\frac{1}{2}$x和y2=$\frac{3}{2}$x为关于y=x的对称函数.(1)判断:①y1=3x和y2=-x;②y1=x+1和y2=x-1;③y1=x2+1和y2=x2-1,其中为关于y=x的对称函数的是①②(填序号)
(2)若y1=3x+2和y2=kx+b(k≠0)为关于y=x的对称函数.
①求k、b的值.
②对于任意的实数x,满足x>m时,y1>y2恒成立,则m满足的条件为m≥-1.
(3)若y1=ax2+bx+c(a≠0)和y2=x2+n为关于y=x的对称函数,且对于任意的实数x,都有y1<y2,请结合函数的图象,求n的取值范围.
分析 (1)根据$\frac{{y}_{1}+{y}_{2}}{2}$=x,可得y1与y2关于y=x对称;
(2)①根据$\frac{{y}_{1}+{y}_{2}}{2}$=x,y1与y2关于y=x对称,可得关于k,b的方程,根据解方程,可得答案;
②根据解不等式,可得答案;
(3)根据$\frac{{y}_{1}+{y}_{2}}{2}$=x,y1与y2关于y=x对称,可得y1,根据解方程组,可得答案.
解答 解:(1)①y1=3x和y2=-x,$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{3x-x}{2}$=x,y1=3x和y2=-x关于y=x对称函数;
②y1=x+1和y2=x-1,$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{x+1+x-1}{2}$=x,y1=x+1和y2=x-1关于y=x对称;
③y1=x2+1和y2=x2-1,$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{{x}^{2}+1+{x}^{2}-1}{2}$=x2≠x,y1=x2+1和y2=x2-1不关于y=x对称;
故答案为:①②;
(2)①y1=3x+2和y2=kx+b(k≠0)为关于y=x的对称函数,得
$\frac{3x+2+kx+b}{2}$=x.
化简,得(3+k)x+(2+b)=2x.
3+k=2,2+b=0.
解得k=-1,b=-2.
②x>m时,y1>y2恒成立,得
3x+2>-x-2.
解得x>-1,
m≥-1,
故答案为:m≥-1;
(3)由y1=ax2+bx+c(a≠0)和y2=x2+n为关于y=x的对称函数,得
$\frac{a{x}^{2}+bx+c+{x}^{2}+n}{2}$=x.
解得a=-1,b=2,c=-n.
对于任意的实数x,都有y1<y2,得
x2+n>-x2+2x-n.
化简,得
x2+n>x,
即x2-x+n>0,
△=(-1)2-4n<0,
解得n>$\frac{1}{4}$.
点评 本题考查了二次函数综合题,利用$\frac{{y}_{1}+{y}_{2}}{2}$=x,可得y1与y2关于y=x对称是解题关键,又利用了解不等式得出m的取值范围;利用不等式无解得出判别式小于零是解题关键.

| A. | 4.6×1010元 | B. | 0.46×1011元 | C. | 46×109元 | D. | 4.6×109元 |
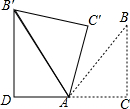 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
| A. | 10 | B. | 4 | C. | 5 | D. | 6 |
| A. | 7 | B. | 8 | C. | 12 | D. | 18 |
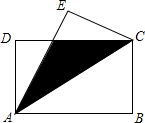 如图,ABCD是长方形,AB=8,BC=6,若将△ABC沿AC对折过来,则B点落到E处,AE交CD于F,求重叠部分的面积.
如图,ABCD是长方形,AB=8,BC=6,若将△ABC沿AC对折过来,则B点落到E处,AE交CD于F,求重叠部分的面积.