题目内容
19.解下列不等式(1)$\frac{2x-1}{3}$≤$\frac{3x+2}{4}$-1
(2)解不等式组$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$.
分析 (1)去分母、去括号、移项、合并同类项,系数化成1即可求解;
(2)首先解每个不等式,两个不等式解集的公共部分就是不等式组的解集.
解答 解:(1)去分母,得4(2x-1)≤3(3x+2)-12,
去括号,得8x-4≤9x+6-12,
移项,得8x-9x≤6-12+4,
合并同类项,得-x≤-2,
系数化成1得x≥2;
(2)$\left\{\begin{array}{l}{4x>2x-6…①}\\{\frac{x-1}{3}≤\frac{x+1}{9}…②}\end{array}\right.$,
解①得x>-3,
解②得x≤2.
则不等式组的解集是-3<x≤2.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
9.下列方程中,有两个相等的实数根的是( )
| A. | x2-4x+4=0 | B. | x2-2x+5=0 | C. | x2-2x=0 | D. | x2-2x-1=0 |
10.下列判断正确的是( )
| A. | “打开电视机,正在播百家讲坛”是必然事件 | |
| B. | “在标准大气压下,水加热到100℃会沸腾”是必然事件 | |
| C. | 一组数据2,3,4,5,5,6的众数和中位数都是5 | |
| D. | “篮球运动员在罚球线上投篮一次,未投中”是不可能事件 |
4.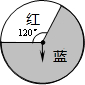 一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )
一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )
 一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )
一个可以自由转动的转盘如图所示,小明已经任意转动这个转盘两次,每次转盘停止转动后指针都落在“蓝色”区域内.那么,从概率的角度分析,小明第三次转动这个转盘,转盘停止时( )| A. | 转出的结果一定是“蓝色” | |
| B. | 转出的结果为“蓝色”的可能性大于“红色” | |
| C. | 转出的结果为“红色”的可能性大于“蓝色” | |
| D. | 转出的结果为“蓝色”和“红色”的可能性一样大 |
8. 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据以上图表信息解答下列问题:
(1)频数分布表中的m=48,n=0.3;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108°;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是$\frac{1}{6}$.
 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 运动项目 | 频数(人数) | 频率 |
| 篮球 | 60 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 72 | n |
| 跳绳 | 36 | 0.15 |
| 其它 | 24 | 0.10 |
(1)频数分布表中的m=48,n=0.3;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为108°;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是$\frac{1}{6}$.
9.下列运算正确的是( )
| A. | 3a3+4a3=7a6 | B. | 3a2•4a2=12a2 | C. | (a+2)2=a2+4 | D. | (a+b)(a-b)=a2-b2 |