题目内容
12．如图，下列条件中，能判定DE∥AC的是（ ）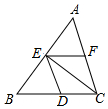
| A． | ∠FEC=∠BCE | B． | ∠FEC=∠FCE | C． | ∠EDC+∠ACB=180° | D． | ∠DEF+∠EDC=180° |
分析 可以从直线DE、AC的截线所组成的“三线八角”图形入手进行判断．
解答 解：∠FEC=∠BCE不是两直线被第三条直线所截得到的，因而不能判定两直线平行；
∠AFE=∠ACD，∠1=∠2是EF和BC被AC所截得到的同位角和内错角，因而可以判定EF∥BC，但不能判定DE∥AC；
∠EDC+∠ACB=180°这两个角是AC与DE被EC所截得到的同旁内角，可以判定DE∥AC．
∠DEF+∠EDC=180°，可以判定EF∥BC，但不能判定DE∥AC；
故选C．
点评 此题考查平行线的判定，关键是根据平行线的判定方法解答．
练习册系列答案
相关题目
如图，A，B在一水池的两侧，若BE=DE，∠B=∠D=90°，点A，E，C在同一条直线上，CD=8cm，则水池宽AB=8m．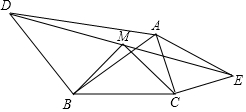
己知：如图，若△ABD和△ACE为等腰Rt△，AB=DB，AC=CE，M为DE中点，求证：△BMC为等腰Rt△．
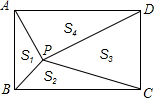如图，点P是矩形ABCD内一点，连接PA、PB、PC、PD，已知AB=3，BC=4，设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4，以下判断：
17．
如图，在等腰三角形ABC中，AB=AC，BD⊥AC，∠ABC=70°，则∠DBC等于（ ）
如图，在等腰三角形ABC中，AB=AC，BD⊥AC，∠ABC=70°，则∠DBC等于（ ）| A． | 20° | B． | 30° | C． | 50° | D． | 70° |
4．
如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1，为边作正方形OB1B2C2，再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3，依此类推…，则正方形OB99B100C100的顶点B100的坐标是（ ）
如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1，为边作正方形OB1B2C2，再以OB1B2C2正方形的对角线OB2为边作正方形OB2B2C3，依此类推…，则正方形OB99B100C100的顶点B100的坐标是（ ）| A． | （2100，0） | B． | （0，250） | C． | （-250，0） | D． | （0，-2100） |
