Question

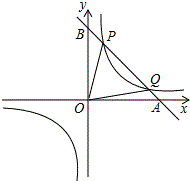如图，已知反比例函数y=

k

x

（k≠0）的图象经过点（

1

2

，8），直线y=-x+b经过该反比例函数图象上的点Q（4，n）．
（1）求上述反比例函数和直线的函数表达式；
（2）若将直线AB向下平移m（m＞0）个单位长度后与反比例函数的图象有且只有一个公共点，求m的值．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：

分析：（1）把已知点代入可求得反比例函数解析式，则可求得Q点，再把Q点坐标代入直线可求得其解析式；
（2）联立直线和反比例函数的解析式，消去y得到关于x的一元二次方程，其判别式=0即可求得m．

解答：解：（1）∵反比例函数y=

k

x

（k≠0）的图象经过点（

1

2

，8），
∴k=

1

2

×8=4，
∴反比例函数解析式为y=

4

x

，
又∵Q点在反比例函数图象上，
∴4n=4，
解得n=1，
∴Q点坐标为（4，1），
∵直线y=-x+b经过点Q，
∴1=-4+b，
解得b=5，
∴直线解析式为y=-x+5；
（2）由题意可设平移后的直线方程为y=-x+5-m，
联立反比例函数解析式，消去y可得：x²+（m-5）x+4=0，
该一元二次方程判别式为△=（m-5）²-16，
直线AB向下平移m（m＞0）个单位长度后与反比例函数的图象有且只有一个公共点时，则有△=0，
即（m-5）²-16=0，解得m=1或9，
故当m=1或9时，直线与反比例函数图象只有一个公共点．

点评：本题主要考查函数图象的交点和待定系数法去函数解析式，利用待定系数法求函数解析式的关键是求得点的坐标，在（2）中把问题转化为一元二次方程根的判别式问题是解题的关键．