题目内容
 如图,已知AB∥CD,AD∥BC,∠1=∠F,∠2=∠E,求∠EOF的度数.
如图,已知AB∥CD,AD∥BC,∠1=∠F,∠2=∠E,求∠EOF的度数.考点:平行线的性质
专题:计算题
分析:根据平行线的性质,由AD∥BC得到∠E=∠ADE,∠F=∠DAF,加上∠1=∠F,∠2=∠E,则∠1=∠DAF,∠2=∠ADE,所以∠DAF=
∠DAB,∠ADE=
∠ADC,
再根据平行线的性质,由AB∥DC得到∠DAB+∠ADC=180°,所以∠DAF+∠ADE=90°,接着根据三角形内角和得到∠AOD=90°,然后利用对顶角的性质得到
∠EOF=90°.
| 1 |
| 2 |
| 1 |
| 2 |
再根据平行线的性质,由AB∥DC得到∠DAB+∠ADC=180°,所以∠DAF+∠ADE=90°,接着根据三角形内角和得到∠AOD=90°,然后利用对顶角的性质得到
∠EOF=90°.
解答:解:∵AD∥BC,
∴∠E=∠ADE,∠F=∠DAF,
∵∠1=∠F,∠2=∠E,
∴∠1=∠DAF,∠2=∠ADE,
∴∠DAF=
∠DAB,∠ADE=
∠ADC,
∵AB∥DC,
∴∠DAB+∠ADC=180°,
∴∠DAF+∠ADE=90°,
∴∠AOD=90°,
∴∠EOF=90°.
∴∠E=∠ADE,∠F=∠DAF,
∵∠1=∠F,∠2=∠E,
∴∠1=∠DAF,∠2=∠ADE,
∴∠DAF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥DC,
∴∠DAB+∠ADC=180°,
∴∠DAF+∠ADE=90°,
∴∠AOD=90°,
∴∠EOF=90°.
点评:本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
 如图,BE和BF三等分∠ABC,CE和CF三等分∠ACB,∠A=75°,求∠F和∠A的关系.
如图,BE和BF三等分∠ABC,CE和CF三等分∠ACB,∠A=75°,求∠F和∠A的关系.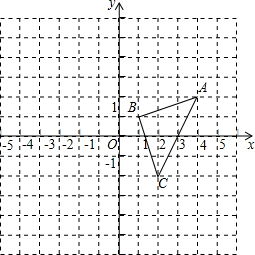 如图,在平面直角坐标系中,已知△ABC的三个顶点A、B、C都在格点上,坐标分别为(4,2),(1,1),(2,-2).
如图,在平面直角坐标系中,已知△ABC的三个顶点A、B、C都在格点上,坐标分别为(4,2),(1,1),(2,-2).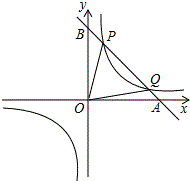 如图,已知反比例函数y=
如图,已知反比例函数y=