题目内容
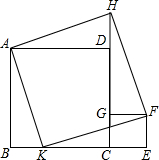 已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形.
已知,如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD到点H,使DH=CE=BK.求证:四边形AKFH是正方形.考点:正方形的判定与性质
专题:证明题
分析:利用正方形的性质结合全等三角形的判定方法得出:△HGF≌△KEF≌△ABK≌△ADH,再利用正方形的判定方法得出答案.
解答: 证明:∵四边形ABCD和CEFG都是正方形,
证明:∵四边形ABCD和CEFG都是正方形,
∴AB=AD=DC=BC,GC=EC=FD=EF,
∵DH=CE=BK,
∴HG=EK=BC=AD=AB,
在△ADH和△ABK中,
,
∴△ADH≌△ABK(SAS),
∴∠HAD=∠BAK.
∴∠HAK=90°,
同理可得:△HGF≌△KEF≌△ABK≌△ADH,
∴AH=AK=HF=FK,
∴四边形AKFH是正方形.
 证明:∵四边形ABCD和CEFG都是正方形,
证明:∵四边形ABCD和CEFG都是正方形,∴AB=AD=DC=BC,GC=EC=FD=EF,
∵DH=CE=BK,
∴HG=EK=BC=AD=AB,
在△ADH和△ABK中,
|
∴△ADH≌△ABK(SAS),
∴∠HAD=∠BAK.
∴∠HAK=90°,
同理可得:△HGF≌△KEF≌△ABK≌△ADH,
∴AH=AK=HF=FK,
∴四边形AKFH是正方形.
点评:此题主要考查了正方形的判定与性质以及全等三角形的判定等知识,得出:△HGF≌△KEF≌△ABK≌△ADH是解题关键.

练习册系列答案
相关题目
2014年金华市实现生产总值(GDP)3206亿元,按可比价计算,比上年增长8.3%.用科学记数法表示2014年金华市的生产总值为( )
| A、32.06×1012元 |
| B、3.206×1011元 |
| C、3.206×1010元 |
| D、3.206×1012元 |
| 17 |
| A、2到3之间 |
| B、3到4之间 |
| C、4到5之间 |
| D、5到6之间 |
若三角形的两边长分别是4cm和3cm,则下列数据中,第三边的长不可能是( )
| A、4cm | B、5cm |
| C、6cm | D、7cm |
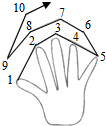 请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢?
请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢? (1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
 如图,在△ABC中,∠ACB=2∠B,∠ACB的平分线交AB于D,DE⊥BC,垂足为E,请写出一对全等三角形,并说明理由.
如图,在△ABC中,∠ACB=2∠B,∠ACB的平分线交AB于D,DE⊥BC,垂足为E,请写出一对全等三角形,并说明理由.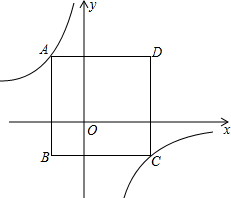 如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=
如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=