题目内容
4.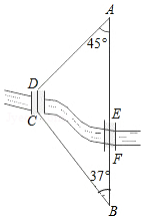 如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.
如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.(1)求点D到直线AB的距离;
(2)现在从A地到B地可比原来少走多少路程?
(结果保留小数点后一位.参考数据:$\sqrt{2}$≈1.41,sin37°≈0.60,cos37°≈0.80).
分析 (1)过点D作DH⊥AB于H,DG∥CB交AB于G,根据平行四边形的判定得出DCBG为平行四边形,在Rt△DGH中,根据DH=DG•sin37,即可求出点D到直线AB的距离;
(2)根据(1)先求出GH、AD和AH的长,再根据两条路线路程之差为AD+DG-AG,代值计算即可得出答案.
解答 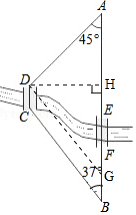 解:(1)如图,过点D作DH⊥AB于H,DG∥CB交AB于G,
解:(1)如图,过点D作DH⊥AB于H,DG∥CB交AB于G,
∵DC∥AB,
∴四边形DCBG为平行四边形.
∴DC=GB,GD=BC=11.
在Rt△DGH中,
DH=DG•sin37°≈11×0.60=6.60,
∴点D到直线AB的距离是6.60km;
(2)根据(1)得:
GH=DG•cos37°≈11×0.80≈8.80,
在Rt△ADH中,
AD=$\sqrt{2}$DH≈1.41×6.60≈9.31.
AH=DH≈6.60,
∵两条路线路程之差为AD+DG-AG,
∴AD+DG-AG=(9.31+11)-(6.60+8.80)≈4.9(km).
即现在从A地到B地可比原来少走约4.9km.
点评 此题考查了解直角三角形的应用,将梯形中的问题转化为三角形问题是解决梯形问题的常用方法,常作的辅助线有平移腰、平移对角线、作高等.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
14.-5的绝对值是( )
| A. | -$\frac{1}{5}$ | B. | 5 | C. | -5 | D. | ±5 |
19.下列四组图形中,一定相似的图形是( )
| A. | 各有一个角是30°的两个等腰三角形 | |
| B. | 有两边之比都等于2:3的两个三角形 | |
| C. | 各有一个角是120°的两个等腰三角形 | |
| D. | 各有一个角是直角的两个三角形 |
9.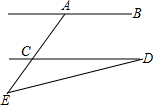 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
 如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )
如图所示,AB∥CD,∠CAB=116°,∠E=40°,则∠D的度数是( )| A. | 24° | B. | 26° | C. | 34° | D. | 22° |
16. 在平面直角坐标系内,作出下列函数的图象.
在平面直角坐标系内,作出下列函数的图象.
(1)如图,y=-x+2.5,填写表,并在图中的坐标系上描点、连线并回答问题.
①当x=3时,y=-0.5;当y=0时,x=2.5.
②图象与x轴的交点坐标是(2.5,0),与y轴的交点坐标是(0,2.5).
③点A(-3,1.5),B(0.5,2)是否在函数图象上?
 在平面直角坐标系内,作出下列函数的图象.
在平面直角坐标系内,作出下列函数的图象.(1)如图,y=-x+2.5,填写表,并在图中的坐标系上描点、连线并回答问题.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 4.5 | 3.5 | 2.5 | 1.5 | 0.5 | … |
②图象与x轴的交点坐标是(2.5,0),与y轴的交点坐标是(0,2.5).
③点A(-3,1.5),B(0.5,2)是否在函数图象上?
 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )


