题目内容
6.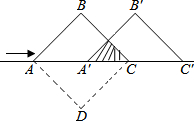 如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )
如图,将两个边长为2cm且互相重叠的正方形纸片,沿对角线AC翻折成等腰直角三角形后,再抽出其中一个等腰直角三角形沿AC移动.若重叠部分(阴影△A′PC)的面积是1cm2,则它移动的距离A A′等于( )| A. | 2cm | B. | $2\sqrt{2}+2$cm | C. | $\sqrt{2}$cm | D. | $2\sqrt{2}-2$cm |
分析 根据正方形的性质求出AC的长,根据平移的性质得到∠A′OC=90°,根据面积公式求出A′C的长即可.
解答 解: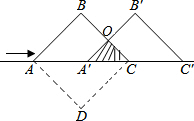 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=2,∠B=90°,
∴AC=2$\sqrt{2}$,
由平移的性质可知,∠A′CO=∠CA′O=45°,
∴∠A′OC=90°,又△A′OC的面积为1,
∴$\frac{1}{2}$×OA′×OC=1,
解得OA′=OC=$\sqrt{2}$,
由勾股定理得,A′C=2,
∴A A′=AC-A′C=2$\sqrt{2}$-2cm,
故选:D.
点评 本题考查的是翻折变换和平移变换的性质,掌握正方形的性质、等腰直角三角形的性质和勾股定理是解题的关键.

练习册系列答案
相关题目
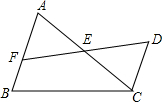 如图,AB∥CD,EF=ED,AB=5,CD=3,则BF=2.
如图,AB∥CD,EF=ED,AB=5,CD=3,则BF=2.