题目内容
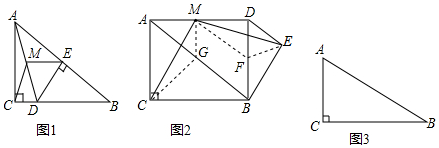
10.如图1,在△ABC中,∠C=90°,点D在BC上,DE⊥AB于点E,点M是AD的中点,连接CM、EM.(1)问题发现:
①线段CM、EM的数量关系是CM=ME;
②∠CME、∠CAB的数量关系是∠CME=2∠CAB.
(2)拓展探究:
将△BED绕着点B旋转到图2的位置时,小明猜想(1)中的结论①②仍然成立,并尝试取AB的中点G和BD的中点F.作了△CGM和△MFE,请你证明小明的猜想.
(3)问题解决:
已知∠B=30°,BD=AC=4,当△BED旋转至A、D、E三点共线时,直接写出线段CM的长.
分析 (1)运用直角三角形斜边中线等于斜边一半,进行分析即可;
(2)运用直角三角形斜边中线等于斜边一半和中位线定理证明全等三角形,进一步得出结论;
(3)运用30°的三角函数求出AB,BE,和AE的长度结合前面结论进一步求解即可.
解答 解:(1)①CM=ME;②∠CME=2∠CAB;
(2)∵AB的中点G和BD的中点F,点M是AD的中点,
∴CG=BG,MG∥BD,MG=$\frac{1}{2}$DB=BF,EF=$\frac{1}{2}$DB=BF,MF=$\frac{1}{2}$AB=BG,
∴∠CGA=2∠ABC,CG=MF,MG=EF,
∵∠CGM=∠CGA+∠AGM=2∠ABC+∠ABD,
∠MFE=∠MFD+∠DFE=∠ABD+2∠DBE,
而∠ABC=∠DBE,
∴∠CGM=∠MFE.
在△CGM和△MFE中,
$\left\{\begin{array}{l}{CG=MF}\\{∠CGM=∠MFE}\\{MG=EF}\end{array}\right.$,
∴△CGM≌△MFE.
∴CM=ME,∠EMF=∠MCG.
∴∠CME=∠CMG+∠GMF+∠EMF=∠CMG+∠MGA+∠MCG
=180°-∠AGC=2∠BAC.
(3)
∵∠B=30°,BD=AC=4,
∴AB=8,BE=2$\sqrt{3}$,DE=2,
如图1,
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=2$\sqrt{13}$,
CM=ME=$\frac{1}{2}$(AE+DE)=$\frac{1}{2}$(2$\sqrt{13}$+2)=$\sqrt{13}$+1,
如图2,
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=2$\sqrt{13}$
CM=ME=$\frac{1}{2}$(AE-DE)=$\frac{1}{2}$(2$\sqrt{13}$-2)=$\sqrt{13}$-1,
综上所述:线段CM的长为:$\sqrt{13}$+1或$\sqrt{13}$-1.
点评 此题主要考查图形的旋转综合问题,知道直角三角形斜边中线等于斜边一半会产生等腰三角形,会用三角形外角的性质,会解直角三角形,能数练证明三角形期全等是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,∠A=36°,AB=AC,BD⊥AC于点D,则∠DBC=( )
如图,在△ABC中,∠A=36°,AB=AC,BD⊥AC于点D,则∠DBC=( )| A. | 8° | B. | 18° | C. | 28° | D. | 44° |
| A. |  | B. |  | C. |  | D. |  |


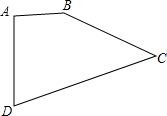 如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积.
如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积.