题目内容
5.计算:(1)3$\sqrt{3}$+2$\sqrt{8}$-$\sqrt{18}$-$\sqrt{48}$;
(2)${(\sqrt{4\frac{1}{2}}-\frac{1}{{\sqrt{2}}})^2}+\sqrt{12}$;
(3)$\frac{{\sqrt{9}}}{{\sqrt{12}}}÷\frac{{\sqrt{3}}}{6}×2\sqrt{\frac{2}{3}}$;
(4)$(\sqrt{27}+2\sqrt{5})(\sqrt{20}-3\sqrt{3})$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先利用完全平方公式计算,然后化简后合并即可;
(3)根据二次根式的乘法法则运算;
(4)先把各二次根式化为最简二次根式,然后利用平方差公式计算.
解答 解:(1)原式=3$\sqrt{3}$+4$\sqrt{2}$-3$\sqrt{2}$-4$\sqrt{3}$
=-$\sqrt{3}$+$\sqrt{2}$;
(2)原式=${(\sqrt{\frac{9}{2}})^2}-2\sqrt{\frac{9}{2}}×\frac{1}{{\sqrt{2}}}+{(\frac{1}{{\sqrt{2}}})^2}+2\sqrt{3}$
=$\frac{9}{2}-2×\frac{3}{2}+\frac{1}{2}+2\sqrt{3}=2+2\sqrt{3}$;
(3)原式=$\sqrt{\frac{9}{12}}×\frac{6}{{\sqrt{3}}}×2\sqrt{\frac{2}{3}}$
=12$\sqrt{\frac{9×2}{12×3×3}}$
=12$\sqrt{\frac{1}{6}}$
=2$\sqrt{6}$;
(4)原式=(2$\sqrt{5}$+3$\sqrt{3}$)(2$\sqrt{5}$-3$\sqrt{3}$)
=(2$\sqrt{5}$)2-(3$\sqrt{3}$)2
=20-27
=-7.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
13. 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=$\frac{15}{4}$.
上面结论正确的有( )
 如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则
如图,将矩形ABCD沿EF折叠,使点B,D重合,已知AB=3,AD=4,则①DE=DF;②DF=EF;③△DCF≌△DGE;④EF=$\frac{15}{4}$.
上面结论正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列运算正确的是( )
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{{{(-2)}^2}}$=2 | C. | $\sqrt{50}$=$\sqrt{25+25}$=5+5=10 | D. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ |
17.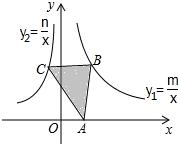 如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
 如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )
如图,已知△ABC,点A在x轴上,点B在双曲线y1=$\frac{m}{x}$(m>0,x>0)上.点C在双曲线y2=$\frac{n}{x}$(n<0,x<0)上.关于△ABC的面积.下列说法中正确的是( )| A. | 当点A保持不动,点C,B随意移动时,△ABC的面积不变 | |
| B. | 当点A移动,BC保持不动时,△ABC的面积不变 | |
| C. | 不管点A,B,C怎么移动,△ABC的面积始终不变 | |
| D. | 不管点A,B,C怎么移动,只要BC与x轴平行,△ABC的面积就不变 |
14.若代数式x+2的值为1,则x等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
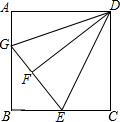 如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.
如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.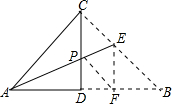 如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=$\sqrt{2}$-1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=$\sqrt{2}$-1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )