题目内容
5.(1)解方程:1+$\frac{3x}{x-2}$=$\frac{6}{x-2}$;(2)解不等式组:$\left\{\begin{array}{l}x-1>2x\\ \frac{1}{2}x+3≤-1.\end{array}$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母,x-2+3x=6,
解得:x=2,
经检验:x=2是原方程的增根,
∴原方程无解;
(2)$\left\{\begin{array}{l}{x-1>2x①}\\{\frac{1}{2}x+3≤-1②}\end{array}\right.$,
由①得,x<-1,
由②得,x≤-8,
∴原不等式组的解集是x≤-8.
点评 此题考查了解分式方程,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
14.下面有理数中,最大的数是( )
| A. | $-\frac{1}{2}$ | B. | 0 | C. | -1 | D. | -3 |
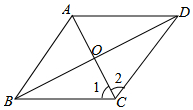 如图,菱形ABCD对角线AC,BD相交于点O,有下列结论:
如图,菱形ABCD对角线AC,BD相交于点O,有下列结论: 如图,在边长为2的正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.
如图,在边长为2的正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.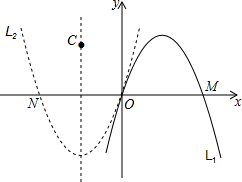 在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.
在直角坐标系xOy中,定义点C(a,b)为抛物线L:y=ax2+bx(a≠0)的特征点坐标.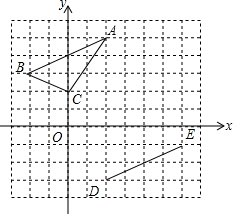 在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1).
在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1). 将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.
将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.