题目内容
16.已知方程a(x-1)+b=2x-c-1至少有两个不同的解,则a2+b2+c2+ab+2bc+ca=7.分析 先将方程变形为(a-2)x-a+b+c+1=0,根据方程a(x-1)+b=2x-c-1至少有两个不同的解,得到方程组$\left\{\begin{array}{l}{a-2=0}\\{-a+b+c+1=0}\end{array}\right.$,求得$\left\{\begin{array}{l}{a=2}\\{b+c=1}\end{array}\right.$,再将a2+b2+c2+ab+2bc+ca变形后整体代入即可求解.
解答 解:a(x-1)+b=2x-c-1,
ax-a+b=2x-c-1,
(a-2)x-a+b+c+1=0,
∵方程a(x-1)+b=2x-c-1至少有两个不同的解,
∴$\left\{\begin{array}{l}{a-2=0}\\{-a+b+c+1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b+c=1}\end{array}\right.$,
∴a2+b2+c2+ab+2bc+ca
=4+b2+c2+2b+2bc+2c
=(b+c)2+2(b+c)+4
=1+2+4
=7.
故答案为:7.
点评 此题主要考查了一元一次方程的解,关键是根据题意得到方程组$\left\{\begin{array}{l}{a-2=0}\\{-a+b+c+1=0}\end{array}\right.$,求得$\left\{\begin{array}{l}{a=2}\\{b+c=1}\end{array}\right.$,同时注意整体思想的应用.

练习册系列答案
相关题目
5. 如图,直线a,b被直线c所截,与∠1是同位角的角是( )
如图,直线a,b被直线c所截,与∠1是同位角的角是( )
 如图,直线a,b被直线c所截,与∠1是同位角的角是( )
如图,直线a,b被直线c所截,与∠1是同位角的角是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
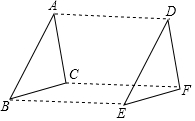 如图,△ABC经过平移后得到△DEF,下列结论:①AB∥DE;②AD=BE;③BC=EF;④∠ACB=∠DFE,其中正确的有( )
如图,△ABC经过平移后得到△DEF,下列结论:①AB∥DE;②AD=BE;③BC=EF;④∠ACB=∠DFE,其中正确的有( ) 如图,在?ABCD中,AB=5cm,AD=8cm,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=3.
如图,在?ABCD中,AB=5cm,AD=8cm,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=3.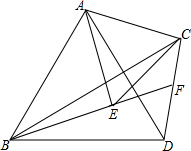 如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,求证:
如图,在△ABC中,分别以AB、AC为边作等边△ABD与等边△ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,求证: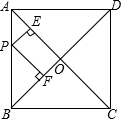 如图,在正方形ABCD中,对角线BD长为18cm,P是AB上任意一点,则点P到AC、BD的距离之和等于9cm.
如图,在正方形ABCD中,对角线BD长为18cm,P是AB上任意一点,则点P到AC、BD的距离之和等于9cm. 如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6,则AC的长等于12.
如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6,则AC的长等于12.