题目内容
6.计算:$\sqrt{(-5)^{2}}$+(2-$\sqrt{5}$)0=6.分析 原式利用平方根定义,以及零指数幂法则计算即可得到结果.
解答 解:原式=5+1=6,
故答案为:6
点评 此题考查了实数的运算,以及零指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.已知$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$≠0,则$\frac{c-a}{b}$的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 3 | D. | $\frac{1}{3}$ |
14.若三角形的两条边的长度是4cm和9cm,则第三条边的长度可能是( )
| A. | 4 cm | B. | 5 cm | C. | 9 cm | D. | 13 cm |
1.已知点A(x1,y1)、B(x2,y2)均在函数y=$\frac{2}{x}$的图象上,若x2<x1<0,则y1、y2的关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法确定 |
11.若关于x的方程ax-b=0(a≠0)的解为x=3,则一次函数y=ax-b(a≠0)的图象与x轴的交点坐标为( )
| A. | (-3,0) | B. | (3,0) | C. | (a,0) | D. | (-b,0) |
18.若不等式组$\left\{\begin{array}{l}3x-a<2\\ x+2b>3\end{array}\right.$的解集是-1<x<2,则a-b的值为( )
| A. | -1 | B. | 2 | C. | 3 | D. | 4 |
15.下列性质中,菱形具有而矩形不一定具有的是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | C. | 对边平行且相等 | D. | 对角线相等 |
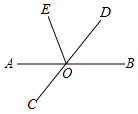 如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠BOE=110°.
如图,直线AB、CD相交于点O,OE是∠AOD的平分线,∠COB=140°,则∠BOE=110°.