题目内容
3.阅读下列材料并填空:(1)探究:平面上有n个点(n≥2)且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?
我们知道,两点确定一条直线.平面上有2个点时,可以画$\frac{2×1}{2}$=1条直线,平面内有3个点时,一共可以画$\frac{3×2}{2}$=3条直线,平面上有4个点时,一共可以画$\frac{4×3}{2}$=6条直线,平面内有5个点时,一共可以画10条直线,…平面内有n个点时,一共可以画$\frac{n(n-1)}{2}$条直线.
(2)运用:某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?
分析 本题要先从简单的例子入手得出一般化的结论,然后根据得出的规律去求特定的值.
解答 解:(1)平面内有5个点时,一共可以画$\frac{5×4}{2}=10$条直线,
平面内有n个点时,一共可以画$\frac{n(n-1)}{2}$条直线;
(2)某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行$\frac{22×21}{2}=231$场比赛,
故答案为:10;$\frac{n(n-1)}{2}$.
点评 此题是探求规律题,读懂题意,找出规律是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
14. 如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
 如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )| A. | 9cm | B. | 6cm | C. | 12cm | D. | 3cm |
11.下列图形中,∠B=2∠A的是( )
| A. |  | B. |  | C. |  | D. |  |
18.一次函数y=mx+|m-1|的图象过点(0,2),且y随x的增大而增大,则m的值为( )
| A. | 3 | B. | 1 | C. | -1 | D. | -1或3 |
12.下列各组数中,能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 4,5,6 | C. | 6,8,11 | D. | 5,12,20 |
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{18}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{18}{5}$. 在如图所示的2017年1月份的月历表中,用一个3×2的长方形框围住相邻三列两行中的6个数字,设其中第一行中间的数字为x.
在如图所示的2017年1月份的月历表中,用一个3×2的长方形框围住相邻三列两行中的6个数字,设其中第一行中间的数字为x.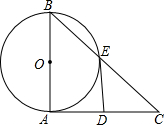 已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,