题目内容
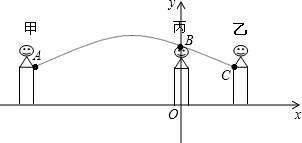
 自从我市实行大课间活动以来,跳大绳成了同学们最喜爱的活动方式,你知道吗?在我们跳大绳时,绳甩到最高处的形状可近似地看为抛物线,如图,正在甩绳的甲、乙两名同学拿绳的手间距离均为4米,手距地面均为1米,同学丙直立在距甲拿绳的手水平距离3米处,其身高为1.5米,当绳子甩到最高处时刚好通过他的头顶(假设在跳绳过程中人的顶部与地面的距离不变).
自从我市实行大课间活动以来,跳大绳成了同学们最喜爱的活动方式,你知道吗?在我们跳大绳时,绳甩到最高处的形状可近似地看为抛物线,如图,正在甩绳的甲、乙两名同学拿绳的手间距离均为4米,手距地面均为1米,同学丙直立在距甲拿绳的手水平距离3米处,其身高为1.5米,当绳子甩到最高处时刚好通过他的头顶(假设在跳绳过程中人的顶部与地面的距离不变).(1)若身高为1.75米的小明同学也在甲、乙之间和丙一同跳,试问这次小明同学在不弯腰的情况下能顺利通过吗?请用学过的知识解决这个问题;
(2)身高为1.33米的小芳也想和丙一同跳,她应该站在什么地方起跳?(精确到0.01米)
考点:二次函数的应用
专题:
分析:(1)设丙所在竖直方向为y轴,水平地面为x轴,根据图象过(1,1),(0,1.5),(-3,1)三点,用待定系数法可求出抛物线解析式.然后令y=1.75时,判断根的判别式符号即可.
(2)根据(1)所求抛物线,利用y=1.33进而求出x的取值范围.
(2)根据(1)所求抛物线,利用y=1.33进而求出x的取值范围.
解答:解:(1)设丙所在竖直方向为y轴,水平地面为x轴,
所求的函数的解析式为y=ax2+bx+c,
由图可知,函数的图象过(-3,1),(0,1.5),(1,1)三点,
则
,
解得:
,
故抛物线解析式为:y=-
x2-
x+
,
当y=1.75,则1.75=-
x2-
x+
,
整理得出:2x2+4x+3=0,
b2-4ac=16-24=-8<0,
故此方程没有实数根,
故这次小明同学在不弯腰的情况下不能顺利通过;
(2)由题意可得出:1.33=-
x2-
x+
,
整理得出:x2+2x-1.02=0,
解得:x1=
≈0.42,x2≈-2.42,
故她应该站在距离丙0.42m或者站在距离丙2.42m的直接的地方都可以.

所求的函数的解析式为y=ax2+bx+c,
由图可知,函数的图象过(-3,1),(0,1.5),(1,1)三点,
则
|
解得:
|
故抛物线解析式为:y=-
| 1 |
| 6 |
| 1 |
| 3 |
| 3 |
| 2 |
当y=1.75,则1.75=-
| 1 |
| 6 |
| 1 |
| 3 |
| 3 |
| 2 |
整理得出:2x2+4x+3=0,
b2-4ac=16-24=-8<0,
故此方程没有实数根,
故这次小明同学在不弯腰的情况下不能顺利通过;
(2)由题意可得出:1.33=-
| 1 |
| 6 |
| 1 |
| 3 |
| 3 |
| 2 |
整理得出:x2+2x-1.02=0,
解得:x1=
-2+
| ||
| 2 |
故她应该站在距离丙0.42m或者站在距离丙2.42m的直接的地方都可以.
点评:本题考查了二次函数的应用,难度较大,此题为数学建模题,借助二次函数解决实际问题是解题关键.

练习册系列答案
相关题目
下列说法错误的是( )
| A、关于某直线对称的两个图形一定能完全重合 |
| B、全等的两个三角形一定关于某直线对称 |
| C、轴对称图形的对称轴至少有一条 |
| D、线段是轴对称图形 |
 如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是( )
如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是( )| A、AB=BC |
| B、∠ACB=60° |
| C、∠B=60° |
| D、AC=BC |
 如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO. 如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由.
如图,在△ABC中,AB=AC=10,BC=16,⊙A的半径为7,判断⊙A与直线BC的位置关系,并说明理由. 如图,点阵中以相邻4个点为顶点的小正方形面积为1.
如图,点阵中以相邻4个点为顶点的小正方形面积为1. 如图,考古学家在一次考古中发现一块破损的圆壁,请你将它复原.
如图,考古学家在一次考古中发现一块破损的圆壁,请你将它复原.