题目内容
如图，在△ABC中，AB=AC=10，BC=16，⊙A的半径为7，判断⊙A与直线BC的位置关系，并说明理由．考点：直线与圆的位置关系
专题：
分析：过A作AD⊥BC，垂足为点D，利用勾股定理求得线段AD的长与⊙O的半径比较后即可确定直线与圆的位置关系．
解答：
解：⊙A与直线BC相交．
过A作AD⊥BC，垂足为点D．
∵AB=AC，BC=16，
∴BD=
BC=
×16=8，
在Rt△ABC中，AB=10，BD=8，
∴AD=
=
=6，
∵⊙O的半径为7，
∴AD＜r，
⊙A与直线BC相交．
解：⊙A与直线BC相交． 过A作AD⊥BC，垂足为点D．
∵AB=AC，BC=16，
∴BD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABC中，AB=10，BD=8，
∴AD=
| AB2-BD2 |
| 102-82 |
∵⊙O的半径为7，
∴AD＜r，
⊙A与直线BC相交．
点评：本题考查了直线与圆的位置关系，解题的关键是求得圆心到直线的距离．
练习册系列答案
相关题目
如图，在一块长a m，宽为b m的长方形草地上，有一条弯曲的小路，小路的左边线向右平移1m就是它的右边线，则这块草地的绿地面积为（ ）| A、（a-1）（b-1） |
| B、a（b-1） |
| C、ab-1 |
| D、（a-1）b |
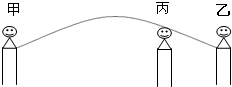自从我市实行大课间活动以来，跳大绳成了同学们最喜爱的活动方式，你知道吗？在我们跳大绳时，绳甩到最高处的形状可近似地看为抛物线，如图，正在甩绳的甲、乙两名同学拿绳的手间距离均为4米，手距地面均为1米，同学丙直立在距甲拿绳的手水平距离3米处，其身高为1.5米，当绳子甩到最高处时刚好通过他的头顶（假设在跳绳过程中人的顶部与地面的距离不变）．