题目内容
14.图1和图2中,优弧$\widehat{AB}$所在⊙O的半径为2,AB=2$\sqrt{3}$,点P为优弧$\widehat{AB}$上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.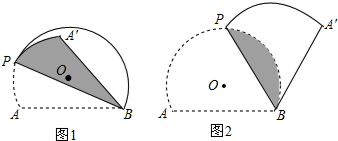
(Ⅰ)点O到弦AB的距离是1,当BP经过点O时,∠ABA′=60;
(Ⅱ)当BA′与⊙O相切时,如图2,求折痕的长.
分析 (1)利用垂径定理和勾股定理即可求出点O到AB的距离;利用锐角三角函数的定义及轴对称性就可求出∠ABA′.
(2)根据切线的性质得到∠OBA′=90°,从而得到∠ABA′=120°,就可求出∠ABP,进而求出∠OBP=30°.过点O作OG⊥BP,垂足为G,容易求出OG、BG的长,根据垂径定理就可求出折痕的长.
解答 解:(1)①过点O作OH⊥AB,垂足为H,连接OB,如图1①所示.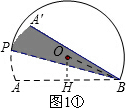
∵OH⊥AB,AB=2$\sqrt{3}$,
∴AH=BH=$\sqrt{3}$.
∵OB=2,
∴OH=1.
∴点O到AB的距离为1.
②当BP经过点O时,如图1②所示.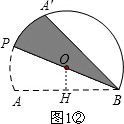
∵OH=1,OB=2,OH⊥AB,
∴sin∠OBH=$\frac{OH}{OB}$=$\frac{1}{2}$.
∴∠OBH=30°.
由折叠可得:∠A′BP=∠ABP=30°.
∴∠ABA′=60°.
故答案为:1、60.
(2)过点O作OG⊥BP,垂足为G,如图2所示.
∵BA′与⊙O相切,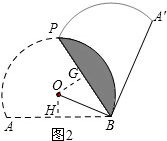
∴OB⊥A′B.
∴∠OBA′=90°.
∵∠OBH=30°,
∴∠ABA′=120°.
∴∠A′BP=∠ABP=60°.
∴∠OBP=30°.
∴OG=$\frac{1}{2}$OB=1.
∴BG=$\sqrt{3}$.
∵OG⊥BP,
∴BG=PG=$\sqrt{3}$.
∴BP=2$\sqrt{3}$.
∴折痕的长为2$\sqrt{3}$.
点评 本题考查了切线的性质、垂径定理、勾股定理、三角函数的定义、30°角所对的直角边等于斜边的一半、翻折问题等知识,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.“五一”假期,某校团委组织500团员前往烈士陵园,开展“缅怀革命先烈,立志为国成才”的活动,由甲、乙两家旅行社来承担此次活动的出行事宜.由于接待能力受限,两家旅行社每家最多只能接待300人,甲旅行社的费用是每人4元,乙旅行社的费用是每人6元,如果设甲旅行社安排x人,乙旅行社安排y人,所学费用为w元,则:
(1)试求w与x的函数关系,并求当x为何值时出行费用w最低?
(2)经协商,两家旅行社均同意对写生施行优惠政策,其优惠政策如表:
如何安排人数,可使出行费用最低?
(1)试求w与x的函数关系,并求当x为何值时出行费用w最低?
(2)经协商,两家旅行社均同意对写生施行优惠政策,其优惠政策如表:
| 人数 | 甲旅行社 | 乙旅行社 |
| 少于250人 | 一律八折优惠 | 七折优惠 |
| 不少于250人 | 五折优惠 |
3.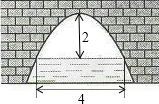 如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
 如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )
如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )| A. | 3 | B. | 2$\sqrt{6}$ | C. | 3$\sqrt{2}$ | D. | 2 |
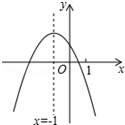 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
 设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点.
设抛物线y=mx2-3mx+2(m≠0)与x轴的交点为A(x1,0),B(x2,0),且x12+x22=17,其中x1<x2,抛物线的顶点为M,点P(a,b)为抛物线上一动点. 如图,矩形ABCD中,AB=2AD,AP平分∠DAB,且AP⊥DP于点P,连接CP,则sin∠DCP的值是$\frac{\sqrt{10}}{10}$.
如图,矩形ABCD中,AB=2AD,AP平分∠DAB,且AP⊥DP于点P,连接CP,则sin∠DCP的值是$\frac{\sqrt{10}}{10}$. 小明把一个含45°角的直角三角板放在如图所示的两条平行线上,测得∠a=130°,则∠β的度数是85°.
小明把一个含45°角的直角三角板放在如图所示的两条平行线上,测得∠a=130°,则∠β的度数是85°.