题目内容
13.若点(-3,y1)和(-1,y2)在函数y=$\frac{1}{3}(x-1)^{2}-2$的图象上,则y1>y2.(填<;>;=)分析 先判断函数的增减性,根据两点的坐标可得出答案.
解答 解:∵y=$\frac{1}{3}(x-1)^{2}-2$,
∴抛物线对称轴为x=-1,开口向上,
∴当x<-1时,y随x增大而减小,
∵-2<-1<1,
∴y1>y2.
故答案为:>.
点评 本题主要考查二次函数的增减性,根据二次函数解析式判断其出增减性是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
3.下列变量之间的关系:
(1)凸多边形的对角线条数与边数;
(2)三角形面积与它的底边(高为定值);
(3)x-y=3中的x与y;
(4)圆的面积与圆的半径;
(5)y=|x|中的x与y.
其中成函数关系的有( )
(1)凸多边形的对角线条数与边数;
(2)三角形面积与它的底边(高为定值);
(3)x-y=3中的x与y;
(4)圆的面积与圆的半径;
(5)y=|x|中的x与y.
其中成函数关系的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.如果点(-2,-3)和(5,-3)都是抛物线y=ax2+bx+c上的点,那么抛物线的对称轴是( )
| A. | x=3 | B. | x=-3 | C. | x=$\frac{3}{2}$ | D. | x=-$\frac{3}{2}$ |
 列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?
列方程解应用题:如图,利用一面长度为9m的墙,用18m长的篱笆,怎样围成一个面积为40m2的矩形场地?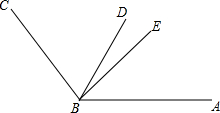 如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数.
如图,BD平分∠ABC,BE将∠ABC分成3:5两部分,∠DBE=15°,求∠ABC的度数.