题目内容
图(1)为已建设封顶的16层楼房和其塔吊图,图(2)为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D点的距离为4m,每层楼高3m,AE、BF、CH都垂直于地面EH,EF=18m,求塔吊的高CH的长.
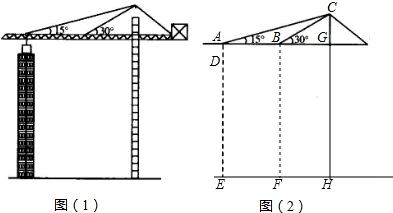

考点:解直角三角形的应用
专题:
分析:根据AD和每层楼的高度,易求得AE、GH的长,关键是求出CG的值.根据三角形的外角性质,易证得△ABC是等腰△,则BC=AB=EF=16m.在Rt△CBG中,已知∠CBG的度数,通过解直角三角形求出CG的长,由此得解.
解答:解:根据题意,得DE=3×16=48m,AB=EF=18m.
∵∠ACB=∠CBG-∠CAB=15°,
∴∠ACB=∠CAB,
∴CB=AB=18m.
∴CG=BC•sin30°=9m,
CH=CG+HG=CG+DE+AD=9+48+4=61(m).
故塔吊的高CH为61米.
∵∠ACB=∠CBG-∠CAB=15°,
∴∠ACB=∠CAB,
∴CB=AB=18m.
∴CG=BC•sin30°=9m,
CH=CG+HG=CG+DE+AD=9+48+4=61(m).
故塔吊的高CH为61米.
点评:此题主要考查的是解直角三角形的应用,能够发现△ABC是等腰三角形是解答此题的关键.

练习册系列答案
相关题目
计算(-3a)3的结果是( )
| A、6a3 |
| B、-27a3 |
| C、8a3 |
| D、-8a3 |
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
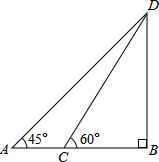 某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(
某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(