题目内容
细观察,找规律.图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3=---------- 度,
图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,
(2)请选择图②证明你填的度数的正确性.
(3)猜想:第n个图中的∠A1+∠A2+∠A3+…+∠An= 度.

(1)图①中的∠A1+∠A2=
图③中的∠A1+∠A2+∠A3+∠A4=
(2)请选择图②证明你填的度数的正确性.
(3)猜想:第n个图中的∠A1+∠A2+∠A3+…+∠An=
考点:平行线的性质
专题:
分析:(1)在①中可直接利用平行线的性质可得出答案,在②中可过A2作A2B∥MA1,结合平行线的性质可得出答案;同理在图③④中可得出答案;
(2)过A2作A2B∥MA1,结合平行线的性质可得出结论;
(3)由(1)(2)可得出答案.
(2)过A2作A2B∥MA1,结合平行线的性质可得出结论;
(3)由(1)(2)可得出答案.
解答:解:(1)∵MA1与NAn平行,
∴在图①可得∠A1+∠A2=180°,
在②中可过A2作A2B∥MA1,如图
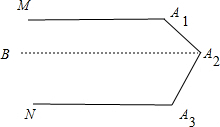
∵MA1∥NA3,
∴A2B∥NA3,
∴∠MA1A2+∠BA2A1=∠BA2A3+∠NA3A2=180°,
∴A1+∠A2+∠A3=360°,
同理可得∠A1+∠A2+∠A3+∠A4=540°,∠A1+∠A2+∠A3+∠A4+∠A5=720°,
故答案为:180;360;540;720;
(2)证明如下:
过A2作A2B∥MA1,如图

∵MA1∥NA3,
∴A2B∥NA3,
∴∠MA1A2+∠BA2A1=∠BA2A3+∠NA3A2=180°,
∴A1+∠A2+∠A3=360°;
(3)结合(1)(2)可得
∠A1+∠A2+∠A3+…+∠An=(n-1)180°,
故答案为:(n-1)180.
∴在图①可得∠A1+∠A2=180°,
在②中可过A2作A2B∥MA1,如图

∵MA1∥NA3,
∴A2B∥NA3,
∴∠MA1A2+∠BA2A1=∠BA2A3+∠NA3A2=180°,
∴A1+∠A2+∠A3=360°,
同理可得∠A1+∠A2+∠A3+∠A4=540°,∠A1+∠A2+∠A3+∠A4+∠A5=720°,
故答案为:180;360;540;720;
(2)证明如下:
过A2作A2B∥MA1,如图

∵MA1∥NA3,
∴A2B∥NA3,
∴∠MA1A2+∠BA2A1=∠BA2A3+∠NA3A2=180°,
∴A1+∠A2+∠A3=360°;
(3)结合(1)(2)可得
∠A1+∠A2+∠A3+…+∠An=(n-1)180°,
故答案为:(n-1)180.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下面从左边到右边的变形是因式分解的是( )
| A、(x+3)(x-3)=x2-9 | ||||||
| B、x2-4+3x=(x-2)(x+2)+3x | ||||||
C、x2+
| ||||||
D、x2-
|
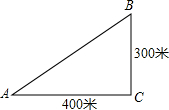 如图,某海滨浴场岸边A处的救生员发现海中B处有人求救,若救生员在岸边行进的速度是8m/s,在海中行进的速度是2m/s,为了节约时间,救生员是直接游向B,还是沿岸边从A处跑到离B最近的点C,然后从点C游向B呢?你能通过计算帮救生员确定营救方案吗?
如图,某海滨浴场岸边A处的救生员发现海中B处有人求救,若救生员在岸边行进的速度是8m/s,在海中行进的速度是2m/s,为了节约时间,救生员是直接游向B,还是沿岸边从A处跑到离B最近的点C,然后从点C游向B呢?你能通过计算帮救生员确定营救方案吗?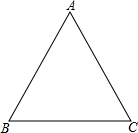 已知:△ABC是等边三角形.
已知:△ABC是等边三角形.