题目内容
先化简,再求值.(-2a4x2+4a3x3-
a2x4)÷(-a2x2),其中a=
,x=-4.
| 3 |
| 4 |
| 1 |
| 2 |
考点:整式的混合运算—化简求值
专题:
分析:根据多项式除以单项式法则算除法,再代入求出即可.
解答:解:(-2a4x2+4a3x3-
a2x4)÷(-a2x2)
=2a2-4ax+
x2,
当a=
,x=-4时,原式=2×(
)2-4×
×(-4)+
×(-4)2=13.
| 3 |
| 4 |
=2a2-4ax+
| 3 |
| 4 |
当a=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
点评:本题考查了整式的混合运算和求值的应用,主要考查学生的计算能力和化简能力,注意运算顺序,难度适中.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,AB、CD相交于O,O是AB的中点,∠A=∠B=80°,若∠D=40°,则∠C=( )
如图,AB、CD相交于O,O是AB的中点,∠A=∠B=80°,若∠D=40°,则∠C=( )| A、40° | B、80° |
| C、60° | D、无法确定 |
 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
若
在实数范围内有意义,则x的取值范围是( )
| x-2 |
| A、x>2 | B、x>3 |
| C、x≥2 | D、x<2 |
一种上衣每件成本为60元,按高出成本价的25%标价出售,后因库存积压,又按标价的80%出售,每件上衣还能盈利( )
| A、0元 | B、1.5元 |
| C、4.8元 | D、5元 |

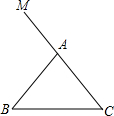 如图,在△ABC中,AB=AC,点M在CA的延长线上.
如图,在△ABC中,AB=AC,点M在CA的延长线上.