题目内容
已知|3a-2|+(1+3b)2=0,求(a-b)2010•(b-a)2011的值.
考点:非负数的性质:偶次方,非负数的性质:绝对值
专题:
分析:根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.
解答:解:∵|3a-2|≥0,(1+3b)2≥0,
又|3a-2|+(1+3b)2=0
∴3a-2=0,1+3b=0,
∴a=
,b=-
.
(a-b)2010•(b-a)2011
=[
-(-
)]2010•(-
-
)2011
=12010•(-1)2011
=-1.
又|3a-2|+(1+3b)2=0
∴3a-2=0,1+3b=0,
∴a=
| 2 |
| 3 |
| 1 |
| 3 |
(a-b)2010•(b-a)2011
=[
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
=12010•(-1)2011
=-1.
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若
在实数范围内有意义,则x的取值范围是( )
| x-2 |
| A、x>2 | B、x>3 |
| C、x≥2 | D、x<2 |
在
、
、π、
、0.505005000中无理数的个数为( )
| ||
| 2 |
| 1 |
| 3 |
| 9 |
| 2 |
| A、2个 | B、3个 | C、4个 | D、5个 |
若x,y为实数,且满足|x-3|+
=0,则(
)2013值是( )
| y+3 |
| x |
| y |
| A、-1 | B、1 | C、2 | D、无法确定 |
 如图,图中的棱柱一共有( )
如图,图中的棱柱一共有( )| A、6个面,12条棱 |
| B、6个面,15条棱 |
| C、7个面,12条棱 |
| D、7个面,15条棱 |
一种上衣每件成本为60元,按高出成本价的25%标价出售,后因库存积压,又按标价的80%出售,每件上衣还能盈利( )
| A、0元 | B、1.5元 |
| C、4.8元 | D、5元 |
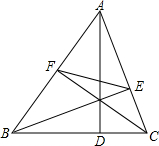 如图,△ABC的三条高为AD、BE、CF,且AB=6,BC=5,EF=3,则sin∠BAC的值为( )
如图,△ABC的三条高为AD、BE、CF,且AB=6,BC=5,EF=3,则sin∠BAC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|

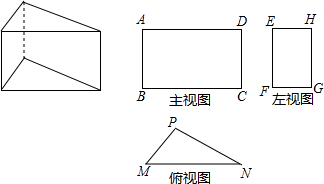 几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=
几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=