题目内容
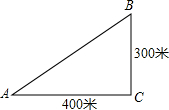 如图,某海滨浴场岸边A处的救生员发现海中B处有人求救,若救生员在岸边行进的速度是8m/s,在海中行进的速度是2m/s,为了节约时间,救生员是直接游向B,还是沿岸边从A处跑到离B最近的点C,然后从点C游向B呢?你能通过计算帮救生员确定营救方案吗?
如图,某海滨浴场岸边A处的救生员发现海中B处有人求救,若救生员在岸边行进的速度是8m/s,在海中行进的速度是2m/s,为了节约时间,救生员是直接游向B,还是沿岸边从A处跑到离B最近的点C,然后从点C游向B呢?你能通过计算帮救生员确定营救方案吗?考点:勾股定理的应用
专题:
分析:先根据勾股定理求出AB的长,再求出由A直接游向B与由A到C再向B的时间,比较其大小即可.
解答:解:∵Rt△ABC中,AC=400米,BC=300米,
∴AB=
=500,
∴从A直接到B所用时间t=
=250秒;
从A到C的时间=
=50秒,从C到B的时间=
=150秒,
∴由A到C在向B的时间=50+150=200秒,
∵250>200,
∴救生员应先跑到C点,再游向B点.
∴AB=
| 4002+3002 |
∴从A直接到B所用时间t=
| 500 |
| 2 |
从A到C的时间=
| 400 |
| 8 |
| 300 |
| 2 |
∴由A到C在向B的时间=50+150=200秒,
∵250>200,
∴救生员应先跑到C点,再游向B点.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
如果两圆的半径分别为2cm和5cm,圆心距为8cm,那么这两个圆的位置关系是( )
| A、外离 | B、外切 | C、相交 | D、内切 |
 如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )
如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
若A=10a2+3b2-5a+5,B=a2+3b2-8a+5,则A-B的值与-9a3b2的公因式为( )
| A、a |
| B、-3 |
| C、9a3b2 |
| D、3a |
若x,y为实数,且满足|x-3|+
=0,则(
)2013值是( )
| y+3 |
| x |
| y |
| A、-1 | B、1 | C、2 | D、无法确定 |

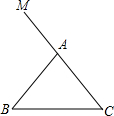 如图,在△ABC中,AB=AC,点M在CA的延长线上.
如图,在△ABC中,AB=AC,点M在CA的延长线上.