题目内容
 如图,在平行四边形ABCD中,AB=60,AD=45,∠A=60°,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,AB=60,AD=45,∠A=60°,求平行四边形ABCD的面积.考点:平行四边形的性质
专题:
分析:过点D作DE⊥AB,根据直角三角形的性质,求得DE,再根据平行四边形的面积计算即可.
解答: 解:过点D作DE⊥AB,垂足为E,
解:过点D作DE⊥AB,垂足为E,
∴∠AED=90°,
∵∠A=60°,
∴∠ADE=30°,
∴AE=
AD,
∵AD=45,
∴AE=
,
∴由勾股定理得DE=
,
∵AB=60,
∴S?ABCD=AB•DE=60×
=135
.
 解:过点D作DE⊥AB,垂足为E,
解:过点D作DE⊥AB,垂足为E,∴∠AED=90°,
∵∠A=60°,
∴∠ADE=30°,
∴AE=
| 1 |
| 2 |
∵AD=45,
∴AE=
| 45 |
| 2 |
∴由勾股定理得DE=
| 45 |
| 2 |
| 3 |
∵AB=60,
∴S?ABCD=AB•DE=60×
| 45 |
| 2 |
| 3 |
| 3 |
点评:本题考查了平行四边形的性质,以及平行四边形的面积、直角三角形的性质,解题关键是求平行四边形的高.

练习册系列答案
相关题目
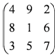 如图,在一个3×3的数阵中,每行、每列数字之和都相同.为使每行、每列数字之和都不相等,至少要改变其中( )个数字.
如图,在一个3×3的数阵中,每行、每列数字之和都相同.为使每行、每列数字之和都不相等,至少要改变其中( )个数字.| A、2种 | B、3种 | C、4种 | D、5种 |