题目内容
19.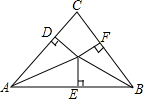 如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.
如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.
分析 根据角平分线的判定定理得到OA平分∠CAB,得到∠OAB=$\frac{1}{2}$∠CAB,同理得到∠OBA=$\frac{1}{2}$∠CBA,根据三角形内角和定理计算得到答案.
解答 解:∵OD=OE,OD⊥AC于D,OE⊥AB于E,
∴OA平分∠CAB,即∠OAB=$\frac{1}{2}$∠CAB,
同理∠OBA=$\frac{1}{2}$∠CBA,
∴∠AOB=180°-(∠OAB+∠OBA)
=180°-$\frac{1}{2}$(∠CAB+CBA)
=180°-$\frac{1}{2}$(180°-∠C)
=130°,
故答案为:130°.
点评 本题考查的是角平分线的判定和三角形内角和定理的应用,掌握到角的两边的距离相等的点在角的平分线上是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
9.甲、乙两家超市为了促销一种定价相同的商品,甲超市连续两次降价10%,乙超市一次性降价20%,则下列说法正确的是( )
| A. | 甲超市与乙家超市一样 | B. | 甲超市比乙家超市便宜 | ||
| C. | 甲超市比乙家超市贵 | D. | 没有具体价格,无法比较 |
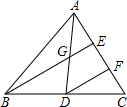 如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.
如图,AD是△ABC的中线,AE=EF=FC,则$\frac{AG}{AD}$=$\frac{1}{2}$,$\frac{GE}{BE}$=$\frac{1}{3}$.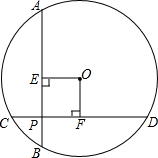 如图所示,⊙O的两条弦AB,CD互相垂直且相交于点P,OE⊥AB,OF⊥CD,垂足分别为E,F,$\widehat{AC}$=$\widehat{BD}$.求证:四边形OEPF是正方形.
如图所示,⊙O的两条弦AB,CD互相垂直且相交于点P,OE⊥AB,OF⊥CD,垂足分别为E,F,$\widehat{AC}$=$\widehat{BD}$.求证:四边形OEPF是正方形.