题目内容
4.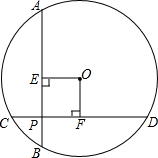 如图所示,⊙O的两条弦AB,CD互相垂直且相交于点P,OE⊥AB,OF⊥CD,垂足分别为E,F,$\widehat{AC}$=$\widehat{BD}$.求证:四边形OEPF是正方形.
如图所示,⊙O的两条弦AB,CD互相垂直且相交于点P,OE⊥AB,OF⊥CD,垂足分别为E,F,$\widehat{AC}$=$\widehat{BD}$.求证:四边形OEPF是正方形.
分析 连接OA、OD.根据矩形的判定定理可以推知四边形OEPF是矩形;根据已知条件$\widehat{AC}$=$\widehat{BD}$可以推知$\widehat{AB}$=$\widehat{CD}$,由圆心角、弧、弦的关系可以证得AB=CD,由垂径定理推知AE=DF,再由勾股定理可得OE=OF;最后根据正方形的判定定理可知矩形OEPF是正方形.
解答 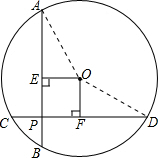 证明:连接OA、OD.
证明:连接OA、OD.
∵AB⊥CD,OE⊥AB,OF⊥CD,
∴四边形OEPF是矩形;
∵$\widehat{AC}$=$\widehat{BD}$,
∴$\widehat{AC}$+$\widehat{BC}$=$\widehat{BD}$+$\widehat{BC}$,即$\widehat{AB}$=$\widehat{CD}$,
∴AB=CD,
∵OE⊥AB,OF⊥CD,垂足分别为E,F,
∴AE=$\frac{1}{2}$AB,DF=$\frac{1}{2}$CD,
∴AE=DF;
∵OA=OD,OE2=OA2-AE2,OF2=OD2-DF2,
∴OE=OF,
∴矩形OEPF是正方形.
点评 本题考查了正方形的判定,圆心角、弧、弦的关系,垂径定理,勾股定理.证明出四边形OEPF是矩形以及OE=OF是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 已知:如图,∠A=∠D=90°,AB=CD,AC与BD相交于点F,E是BC的中点.求证:∠BFE=∠CFE.
已知:如图,∠A=∠D=90°,AB=CD,AC与BD相交于点F,E是BC的中点.求证:∠BFE=∠CFE.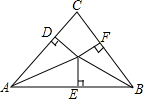 如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.
如图,OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,且OD=OE=OF,若∠C=80°,则∠AOB=130°.