题目内容
6. 如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )
如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )| A. | 720° | B. | 360° | C. | 180° | D. | 540° |
分析 连接AC,根据平行线的性质由AB∥CD得到∠BAC+∠DCA=180°,再由四边形内角和定理得∠2+∠3+∠EAC+∠FCA=360°,然后把两式相加即可得到∠1+∠2+∠3+∠4=540°.
解答 解:连接AC,如图,
∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵∠2+∠3+∠EAC+∠FCA=360°,
∴∠2+∠3+∠EAC+∠FCA+∠BAC+∠DCA=540°,
即∠1+∠2+∠3+∠4=540°.
故选D.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
14.若$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$(a≠0)是方程2x+y=0的一个解,则( )
| A. | a和b同号 | B. | a和b异号 | ||
| C. | a和b可能同号也可能异号 | D. | a≠0,b=0 |
15.在$\frac{1}{x}$、$\frac{1}{2}$、$\frac{{{x^2}+1}}{2}$、$\frac{3xy}{π}$、$\frac{3}{x+y}$、$a+\frac{1}{b}$中,分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
16.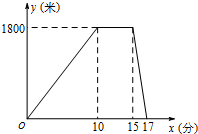 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中正确的是( )| A. | 小明在公园休息了15分钟 | B. | 小明乘出租车用了17分 | ||
| C. | 小明跑步的速度为120米/分 | D. | 出租车的平均速度是900米/分 |
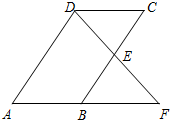 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.