题目内容
17．若实数a、b满足a+b=0，且a＜b，则一次函数y=ax+b的图象不可能经过（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 先根据a+b=0得出a=-b，再由a＜b可知a≤0，b≥0，根据一次函数的图象与系数的关系即可得出结论．
解答 解：∵a+b=0，
∴a=-b．
∵a＜b，
∴a≤0，b≥0．
∵a是一次函数的系数，
∴a≠0，b≠0，
∴a＜0，b＞0，
∴一次函数y=ax+b的图象经过一二四象限，不经过第三象限．
故选C．
点评 本题考查的是一次函数的图象与系数的关系，熟知一次函数y=kx+b（k≠0）中，当k＜0，b＞0时函数的图象在一、二、四象限是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
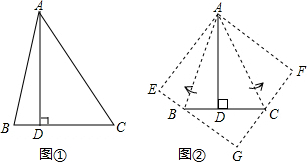
如图，直线a与直线b被直线c所截，b⊥c，垂足为点A，∠1=70°，若使直线b与直线a平行，则可将直线b绕着点A顺时针至少旋转20度．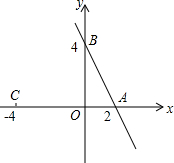
如图，直线y=-2x+b与x轴，y轴分别相交于A、B两点，点B的坐标为（0，4），点C的坐标为（-4，0）．
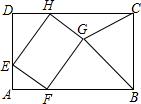如图，矩形ABCD中，AD=6，CD=6+$2\sqrt{2}$，E为AD上一点，且AE=2，点F，H分别在边AB，CD上，四边形EFGH为矩形，点G在矩形ABCD的内部，则当△BGC为直角三角形时，AF的值是2或4．
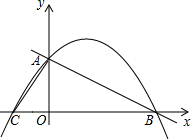如图，在直角坐标系中，已知直线y=-$\frac{1}{2}$x+4与y轴交于A点，与x轴交于B点，C点的坐标为（-2，0）．
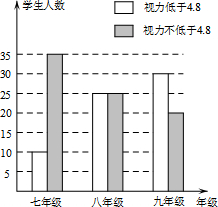在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图．请根据图中信息解决下列问题：