题目内容
9.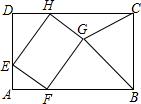 如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.
如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.
分析 如图过点G作MN⊥AB垂足为M,交CD于N,作GK⊥BC于K,先证明△HNG≌△FAE,得到AE=NG=2,ED=GM=4,再由△CGK∽△GBK得到$\frac{CK}{GK}$=$\frac{GK}{BK}$,GK=MB=CN=2$\sqrt{2}$,由△AEF∽△MFG,得到$\frac{AE}{MF}$=$\frac{AF}{MG}$,列出方程即可解决问题.
解答 解:如图过点G作MN⊥AB垂足为M,交CD于N,作GK⊥BC于K.
∵四边形EFGH是矩形,
∴GH=EF,GH∥EF,∠A=90°,
∴∠DNM+∠NMA=90°,
∴∠AMN=∠DNM=90°,
∵CD∥AB,
∴∠NHG=∠AFE,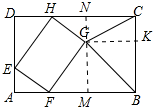
在△HNG和△FAE中,
$\left\{\begin{array}{l}{∠HNG=∠FAE}\\{∠NHG=∠AFE}\\{GH=EF}\end{array}\right.$,
∴△HNG≌△FAE,
∴AE=NG=2,ED=GM=4,
∵四边形NGKC、四边形GMBK都是矩形,
∴CK=GN=2,BK=MG=4,
当∠CGB=90°时,∵△CGK∽△GBK,
∴$\frac{CK}{GK}$=$\frac{GK}{BK}$,
∴GK=MB=CN=2$\sqrt{2}$,
∴DN=AM=AB-MB=6,
∴四边形AMND是正方形,设AF=x,则FM=6-x,
∵△AEF∽△MFG,
∴$\frac{AE}{MF}$=$\frac{AF}{MG}$,
∴$\frac{2}{6-x}$=$\frac{x}{4}$
∴x2-6x+8=0,
∴x=2或4.
∴AF=2或4.
故答案为2或4
点评 本题考查矩形的性质、全等三角形得到和性质、相似三角形的判定和性质,解题的关键是添加辅助线,构造全等三角形或相似三角形,学会转化的思想,把问题转化为方程去思考,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,已知AD∥BC,∠1=∠2,说明BE∥DF的理由.
如图,已知AD∥BC,∠1=∠2,说明BE∥DF的理由.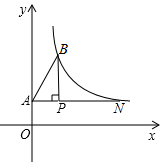 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,作PB⊥AP交反比例函数y=$\frac{k}{x}$(x>0)于点B,连结AB.已知tan∠BAP=$\frac{3}{2}$.
 如图所示,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=55°.
如图所示,一个宽度相等的纸条按如图所示方法折叠一下,则∠1=55°.