题目内容
1. 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)在图中确定该圆弧所在圆的圆心D点的位置,D点坐标为(2,0).
(2)连接AD、CD,求⊙D的半径及弧$\widehat{AC}$的长.
分析 (1)利用垂径定理可作AB和BC的垂直平分线,两线的交点即为D点,可得出D点坐标;
(2)在△AOD中AO和OD可由坐标得出,利用勾股定理可求得AD和CD,即为⊙D的半径;过C作CE⊥x轴于点E,则可证得△OAD≌△EDC,可得∠ADO=∠DCE,可得∠ADO+∠CDE=90°,可得到∠ADC的度数,利用弧长公式可得结果.
解答 解:(1)如图1,分别作AB、BC的垂直平分线,两线交于点D,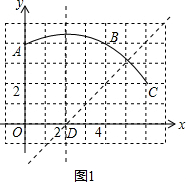
∴D点的坐标为(2,0),
故答案为:(2,0);
(2)如图2,连接AD、CD,过点C作CE⊥x轴于点E,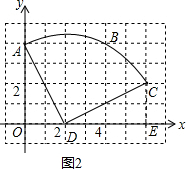
则OA=4,OD=2,在Rt△AOD中,可求得AD=2$\sqrt{5}$,
即⊙D的半径为2$\sqrt{5}$,
且CE=2,DE=4,
∴AO=DE,OD=CE,
在△AOD和△DEC中,
$\left\{\begin{array}{l}{AO=DE}\\{∠AOD=∠CDE}\\{OD=CE}\end{array}\right.$,
∴△AOD≌△DEC(SAS),
∴∠OAD=∠CDE,
∴∠CDE+∠ADO=90°,
∴∠ADC=90°,
弧AC的长=$\frac{90}{180}$π×2$\sqrt{5}$=$\sqrt{5}$π.
点评 本题主要考查垂径定理和全等三角形的判定和性质、扇形等知识的综合应用,掌握确定圆心的方法,即确定出点D的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知某种儿童米粉的标准质量为200g,苏果超市从购进的儿童米粉中随机抽取8袋检测每袋的质量是否符合标准质量,超过与不足的质量分别用正、负数表示,例如+2表示该袋米粉超过标准质量2g,现记录如表:
(1)指出编号为几的米粉最接近标准质量?
(2)在抽取的八袋米粉中最重的那袋比最轻的那袋多多少克?
(3)这次抽样的八袋米粉的总质量是多少?
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 偏差 | +1 | -2 | -1 | -2 | -0.5 | +4 | +2 | -1 |
(2)在抽取的八袋米粉中最重的那袋比最轻的那袋多多少克?
(3)这次抽样的八袋米粉的总质量是多少?