题目内容
15．两年前生产1吨甲种药品的成本是5000元．随着生产技术的进步，成本逐年下降，第2年的年下降率是第1年的年下降率的2倍，现在生产1吨甲种药品成本是2400元．为求第一年的年下降率，假设第一年的年下降率为x，则可列方程（ ）| A． | 5000（1-x-2x）=2400 | B． | 5000（1-x）2=2400 | ||
| C． | 5000-x-2x=2400 | D． | 5000（1-x）（1-2x）=2400 |
分析 若这种药品的第一年平均下降率为x，则第二年的年下降率为2x，根据两年前生产1吨某药品的成本是5000元，随着生产技术的进步，现在生产1吨药品的成本是2400元可列方程．
解答 解：设这种药品的年平均下降率为x，则第二年的年下降率为2x，
根据题意得：5000（1-x）（1-2x）=2400．
故选D．
点评 本题考查增长率问题，发生了两年变化，知道两年前为5000，两年后为2400，设出下降率即可列出方程．
练习册系列答案
相关题目
5．
如图，在直角坐标系xOy中，A（-4，0），B（0，2），连结AB并延长到C，连结CO，若△COB∽△CAO，则点C的坐标为（ ）
如图，在直角坐标系xOy中，A（-4，0），B（0，2），连结AB并延长到C，连结CO，若△COB∽△CAO，则点C的坐标为（ ）| A． | （1，$\frac{5}{2}$） | B． | （$\frac{4}{3}$，$\frac{8}{3}$） | C． | （$\sqrt{5}$，2$\sqrt{5}$） | D． | （$\sqrt{3}$，2$\sqrt{3}$） |
6．tan30°的结果等于（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{1}{2}$ |
3．
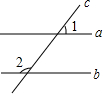如图，平行线a，b被直线c所截，∠1=42°38′，则∠2的度数为（ ）
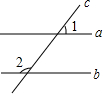如图，平行线a，b被直线c所截，∠1=42°38′，则∠2的度数为（ ）| A． | 157°62′ | B． | 137°22′ | C． | 137°62′ | D． | 47°22′ |
10．若$\sqrt{a+b+5}$+|2a-b+1|=0，则（b-a）2016的值为（ ）
| A． | -1 | B． | 1 | C． | 52015 | D． | -52015 |
20．下列各式正确的是（ ）
| A． | 20=0 | B． | |-$\sqrt{2}$|=$\sqrt{2}$ | C． | $\sqrt{4}$=±2 | D． | -22=4 |
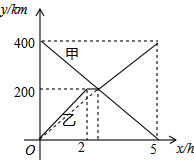甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车出发2h后休息，与甲车相遇后，继续行驶．设甲、乙两车与B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲、y乙与x之间的函数图象如图所示，结合图象解答下列问题：
5．有3个整式x，x+1，2，先随机取一个整式作为分子，再在余下的整式中随机取一个作为分母，恰能组成成分式的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |